基于 0-1 规划模型旅游团路线的设计

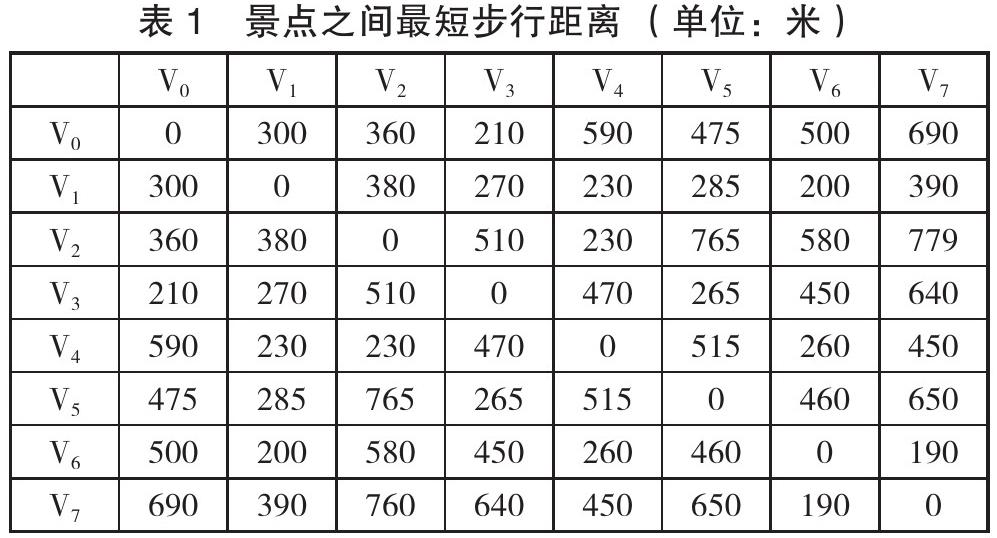
摘要：基于 0-1 规划模型设定目标函数与约束条件，并通过 LINGO 软件求解，给出了游览潘安湖 7 个景点，每个景点至少游览一次的最短路径安排。景点在有游览时间和开放时间的限制下，通过增加约束条件，给出了三个旅游团景点游览最大时长的路线安排。

关键词：0-1 规划 旅游团 最短路

一、引言

随着中国经济的快速发展，旅游产业在以更迅勐的速度前进。当下越来越多的人选择空闲的时间去旅游，而报团旅游成为多数人的一个选择。对于旅游团组织者来说设计一个合理的旅游线路，使旅游者能够以最短的时间获得最大的观赏效果尤为重要。笔者以徐州潘安湖风景区为例，以最短路模型设计最优的旅游线路。

潘安湖景区有游客服务中心、阳光草坪等 7 个景点，景点之间最短步行距离如表 1 所示。现有两个问题：问题 1 游客从 V0 景石出发，步行游览 V1 游客服务中心，V2 阳光草坪，V3 森林小剧场，V4 儿童科普体验区，V5 儿童戏水场，V6 湿地博物馆，V7 湿地商业街，找出一条以 V0 景石为起点，以 V7 湿地商业街为终点的最短路线，并且要求 V1-V7 每个景点至少经过一次；问题 2 现在有三个旅游团同时到潘安湖景区旅游，V1-V6 每个景点在同一时间只能接待一个旅游团，即在某一景点后到的旅游团需等前面的旅游团游览完才能游览，三个旅游团步行的速度是一定的，同时 V3 森林小剧场，只有整点或半点才能开放，若三个旅游团第一个参观的景点为 V3 则必然有等待时间，旅游团在每个景点的游览时间在一定时间范围内可调节，为使在景点的游览时间最长，给出三个旅游团的浏览路线。

二、问题分析

对于问题 1，已知任意两个景点之间的最短步行距离，寻找从景石到湿地商业街的最短路线，且中间要经过 V1-V6 至少一次，景点游览的顺序不同，路线的长短也会不同。此问题看似和最短路问题相似，但不是最短路问题，最短路问题是求起点到终点的最短路，给出的中间点可以不全部通过，但此问题设定的是 V1-V6 至少要通过一次，所有的点通过一次，这类问题又和哈密尔顿圈问题相似，但哈密尔顿圈问题是经过所有的点最终要回到原点，这里我们所有的点不回到原点。因此，我们需要对哈密尔顿圈问题进行适当的改进以此来解决此问题。这里采用 0-1 规划模型[1-2]，以所有的点连接距离最短为目标函数，添加相应的等式作为约束条件，用 LINGO 软件求解此问题。

对于问题 2，三个旅游团在其中游览，为使三个旅游团在景点总的游览时间达到最长，应该使在景点间走路的时间最短，同时应尽量错开旅游团在同一景点同一时间的游览，以避免等待时间。目标函数依旧为游览所有的景点距离最短，以此来使景点间走路时间最短，同时约束条件应增加限制，错开各旅游团的路线，利用可在某个景点游览时间的长短，错开两个旅游团在同一个景区的等待时间，使游览时间达到最长。

三、模型建立与求解

（一）问题 1 模型的建立与求解

用表示景点 i 与景点 j 之间的距离，引入 0—1 变量，表示从景点 i 到景点 j 的路线在最短路径上，表示该路线不在最短路径上。

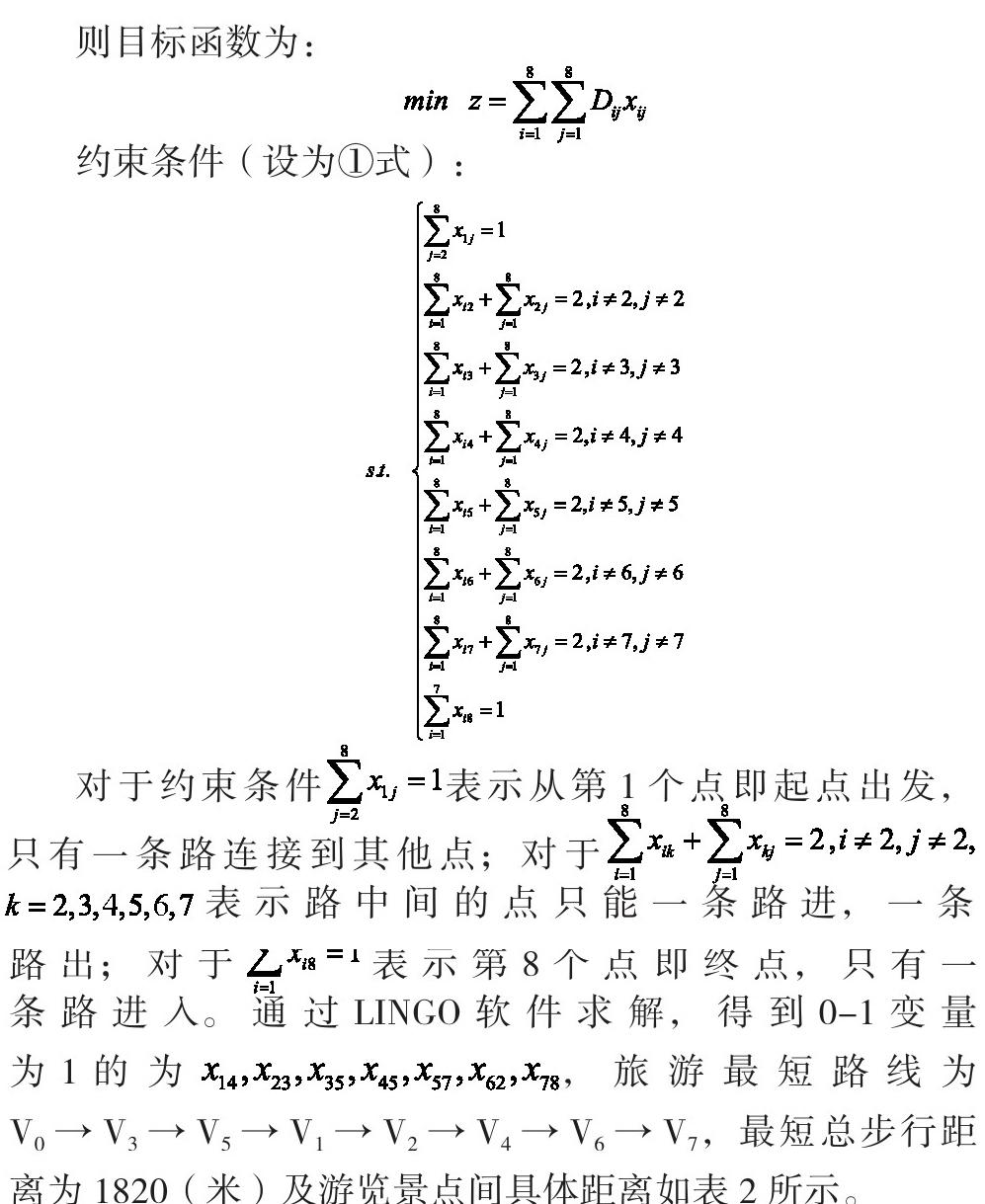
则目标函数为：

约束条件（设为 ① 式）：

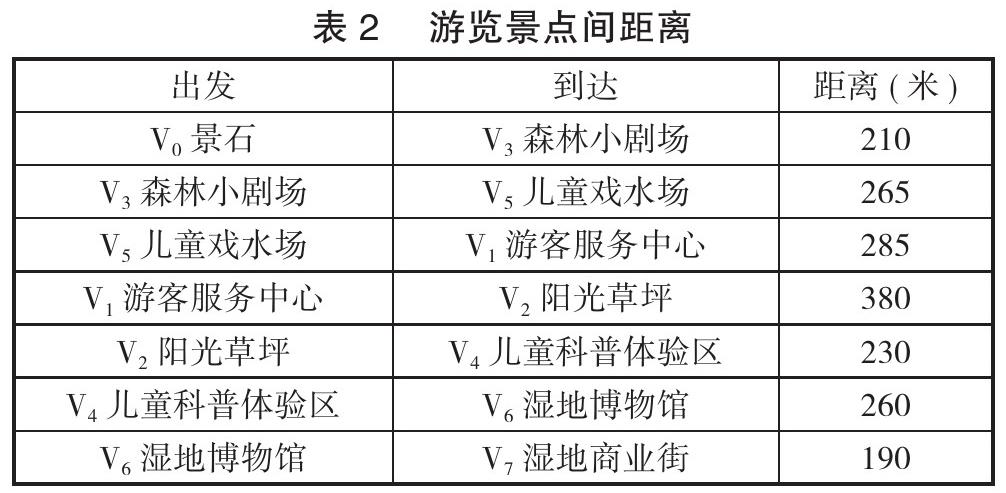
对于约束条件表示从第 1 个点即起点出发，只有一条路连接到其他点；对于表示路中间的点只能一条路进，一条路出；对于表示第 8 个点即终点，只有一条路进入。通过 LINGO 软件求解，得到 0-1 变量为 1 的为，旅游最短路线为 V0→V3→V5→V1→V2→V4→V6→V7，最短总步行距离为 1820（米）及游览景点间具体距离如表 2 所示。

（二）问题 2 模型的建立与求解

若想增大旅游团在景点的游览时间，必须要缩短在景点间的步行时间。游客步行速度是一定的，因此为游客设计最大的景点游览时间线路，就是设计从景石出发到湿地商业街的最短路径。问题 1 给出了从景石出发到湿地商业街的最短路径，现在有三个旅游团对景点进行游览，并且森林小剧场只有整点或者半点开放。问题 1 最短旅游路线从景石出发第一个旅游点为森林小剧场，由于森林小剧场是半点或整点开放，若第一个游览点为森林小剧场必然会等待，因此旅行团第一个点不应该经过森林小剧场，为此应增加约束，在 ① 式基础上增加 x14=0 这个约束，于是第一个旅游团目标函数：

约束条件：

通过 LINGO 软件求解，可得变量 x13，x27，x35，x46，x54，x62，x78 为 1，所以第一个旅游团的行走线路为 V0 景石 V2 阳光草坪 V4 儿童科普体验区 V3 森林小剧场 V5 儿童戏水场 V1 旅游服务中心 V6 湿地博物馆 V7 湿地商业街。

对于第二旅游团来说，第一个游览的点不能为森林小剧场，同时为了不等待第一个旅游团第一个游览的点，因此第二旅游团第一个不能浏览的点也就是阳光草坪，因此约束条件在 ① 式基础上增加约束：x14=0，x13=0。通过 LINGO 软件求解，可得变量 x12，x26，x35，x43，x57，x64，x78 为 1，在第二个旅游团第一个点不游览森林小剧场和阳光草坪的条件下，最短旅游路线为：V0 景石 V1 旅游服务中心 V5 儿童戏水馆 V3 森林小剧场 V2 阳光草坪 V4 儿童科普体验区 V6 湿地博物馆 V7 湿地商业街。

对于第三个旅游团，和第二个旅游团类似，第一个游览的点不能为森林小剧场，同时也不能为第一个旅游团第一个游览的点与第二个旅游团第一个游览的点，即不能为阳光草坪与旅游服务中心，因此约束条件在 ① 式基础上增加约束：x14=0，x13=0，x12=0。 通过 LINGO 软件求解，可得变量 x16，x27，x43，x52，x64，x78 为 1，即第三个旅游团的最短旅游路线为：V0 景石 V5 儿童戏水场 V3 森林小剧场 V2 阳光草坪 V4 儿童科普体验区 V1 游客服务中心 V6 湿地博物馆 V7 湿地商业街。

四、结语

旅游团安排路线是一个较为复杂的问题，本文基于 0-1 规划模型给出将所有的景点都至少经过一次的最短路径，并给出了三个旅游团旅游的时间安排。本模型还可以推广到 n 个景点的最短路设计，以及 m 个旅游团的游览安排。此模型利用 LINGO 软件求解方便准确，以此安排旅游路线，提高了游客的游玩效率，便于旅游团旅行安排。

参考文献：

[1] 谢金星，薛毅.优化建模与 LINDO/LINGO 软件[M].北京：清华大学出版社，2005.

[2] 韩中庚.数学建模方法及其应用（第二版）[M].北京：高等教育出版社，2009.

基金项目：浙江机电职业技术学院教育教学改革重点培育项目「高职高等数学趣味化教学探究」（编号：A015218314）。

（作者单位：浙江机电职业技术学院）

作者 董飞