基于 ARMA 模型对我国金融机构存款的预测研究

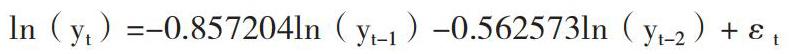
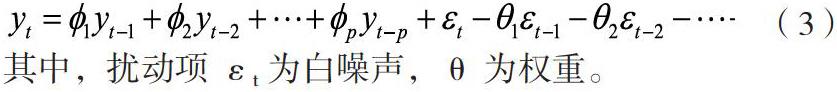
摘要：近年来，随着我国经济的快速发展，我国金融机构各项存款也有了较快的发展。为了较为准确地对我国金融机构存款进行预测和分析，本文选取 2000 年 1 月至 2018 年 2 月我国金融机构各项存款总和按月统计的数据，对比分析了 OLS 回归预测的结果，再应用 ARMA 模型进行时间序列建模分析，对我国金融机构存款进行了比较准确合理的短期预测，对宏观经济政策调控、金融机构进行存款结构调整、居民参与金融活动选择等具有一定的参考价值。

关键词：金融机构存款 ARMA 模型 OLS 回归模型预测

一、引言

随着我国经济的快速发展，金融机构存款也有了较快增长。对于营利性金融机构来说，存款业务是经营的核心业务，是金融机构增强自身的盈利能力、提升自身的区域影响力的先决条件和关键环节。从期限结构看，活期存款的下降和各项存款定期化走势明显是当前我国金融机构存款大幅少增的原因；从金融投资行为看，居民选择股票、理财、信托产品等其他金融资产对金融机构存款起到了分流作用[1，2]。

闫静文，张晋伟（2015）研究发现金融机构各项存款增速的明显下滑制约了金融机构的信贷规模[3]。RuiHan，MartinMelecky（2016）从国际金融统计的角度，利用跨国数据对全球银行存款增长中储蓄的增长进行研究，得出更多的人选择正规储蓄产品可以使该国的银行体系享有更稳定的存款资金的重要结论[4]。

徐煜程（2017）通过对比分析 OLS 回归预测的结果，再应用 ARMA 模型进行时间序列分析，比较准确地预测了 2016 年 11 月的金融机构存款[5]。

研究我国金融机构存款，对国家宏观经济政策的出台、金融市场制度的完善、金融市场的改革等具有重要的意义；对我国金融机构进行存款结构的选择和调整，提高其在金融市场中的竞争力具有重要的参考价值。

二、金融机构存款

（一）金融机构的定义及范围界定

金融机构作为金融体系的一部分，是指在金融市场中专门从事金融活动，在经济金融活动中为资金盈余者和资金需求者提供条件、促使资金融通实现，为社会中的法人机构和自然人以及政府部门提供金融服务的金融中介机构，也常常称为金融中介、金融中介机构。

本文中的金融机构包括中国人民银行、银行业存款类金融机构、银行业非存款类金融机构。其中，银行业存款类金融机构包括银行、信用社和财务公司，银行业非存款类金融机构包括信托投资公司、金融租赁公司、汽车金融公司和贷款公司等。

（二）存款的定义及金融机构存款的范围

存款指企业、机关、团体或居民根据资金必须收回的原则，把货币资金存入银行或其他信贷机构保管并取得一定利息的一种信用活动形式。根据存款对象或性质的不同可划分为单位存款、个人存款、财政性存款、临时性存款、委托存款、其他存款等科目。它是银行信贷资金的主要来源。

金融机构资金来源各项存款包括境内存款和境外存款，境内存款包括住户存款、非金融企业存款以及政府存款，前二者均分类为活期存款、定期及其他存款，政府存款则分为财政性存款和机关团体存款。自 2015 年起，「各项存款」含非银行业金融机构存放款项。

三、ARMA 模型

（一）ARMA 模型简介

ARMA 模型是由美国统计学家 G.E.P.Box 和英国统计学家 G.M.Jenkins 在 20 世纪 70 年代提出的时序分析模型，即自回归移动平均模型，它是由自回归模型（简称 AR 模型）与滑动平均模型（简称 MA 模型）为基础混合构成的，是研究时间序列的重要方法。若时间序列 y t 是它的当前与前期的随机误差项以及它的前期值的线性函数，则可以表示为：

称该时间序列为（p，q）阶的自回归移动平均模型，记为 ARMA（p，q）。其中，1，2，…p 为自回归系数，θ1，θ2，…θq 为移动平均系数，都是模型的待估参数。

（二）ARMA 模型的预测特点

ARMA 模型有着广泛的应用，与其他预测分析方法相比，此方法认为：在一个较短的时期内，可各影响因素对预测指标的影响规律及这些经济因素本身的变动趋势是不变的，因此，利用预测指标历史数据进行预测能够保证一定的预测精度。而且由于 ARMA 预测模型不直接考虑其他相互因素的变动，预测方法比较简明，适合用于进行指标数量不大，但预测频度较高的预测工作。

因此，ARMA 模型适用于单指标的预测工作，它对资料的要求比较单一，只需要变量本身的历史数据，在实际应用中有着广泛的适用性，对于提高分析的预见性、制定合理有效的宏观政策都有重要的意义。

三、我国金融机构存款预测研究的建模分析

（一）数据选取与处理

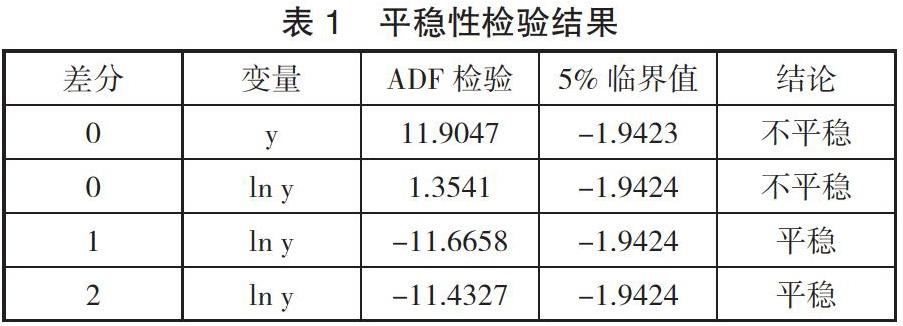
本研究选取中国国家统计局（http：//data.stats.gov.cn/staticreq.htm）金融机构信贷收支统计金融机构人民币信贷收支表中的各项存款作为研究的数据来源，收集并整理出 2000 年 1 月到 2018 年 2 月共 218 个月度数据，数据处理均采用 Eviews 软件完成。由我国金融机构存款数据的走势图可以初步判断该序列为不平稳时间序列，为消除数据异方差的同时又不改变数据的相对关系，故对我国金融机构存款取对数并进行单位根检验。检验结果如下表 1：

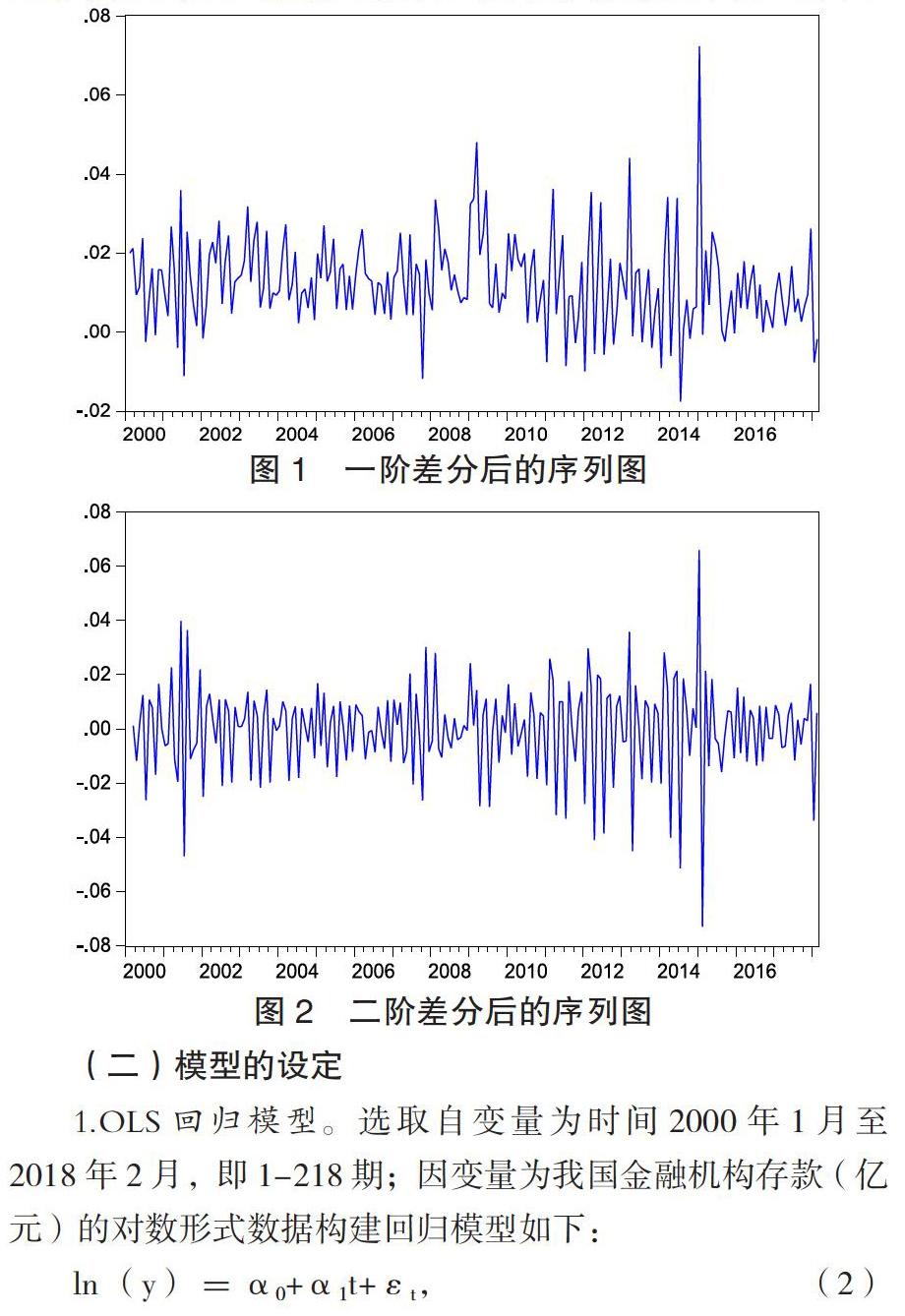
由检验结果可知，金融机构存款的对数序列没有通过单位根检验，即该序列为存在单位根的不平稳时间序列，需对其进行差分处理。经过一阶差分和二阶差分后，该序列已经基本平稳且在零均值附近波动。差分结果如图 1、图 2 所示：

（二）模型的设定

1.OLS 回归模型。选取自变量为时间 2000 年 1 月至 2018 年 2 月，即 1-218 期；因变量为我国金融机构存款（亿元）的对数形式数据构建回归模型如下：

2. ARMA 模型。AR 为一阶自回归模型，而 MA 为移动平均模型，为了更好的对数据进行拟合，可将其结合起来，得到 ARMA 模型，具体如下：

其中，扰动项 εt 为白噪声，θ 为权重。

（三）模型估计

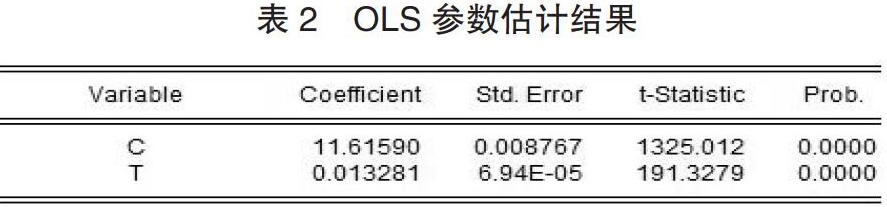
1.OLS 模型。假定所建模型及其中的随机扰动项 εt 满足各种古典假定，可以用 OLS 法估计其未知参数，估计结果如下表 2：

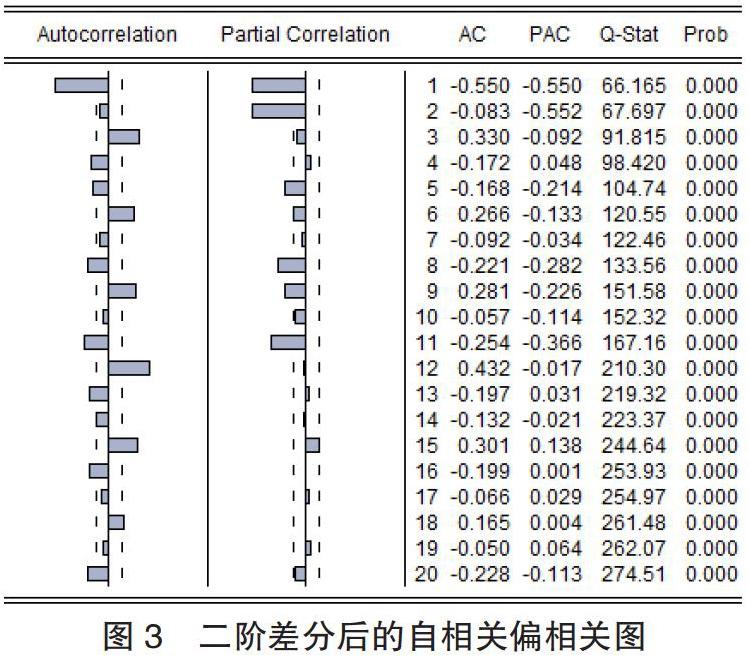
2. ARMA 模型。通过 Eviews 做出二阶差分过后的自相关偏相关图 3，由图可知此序列自相关函数呈现拖尾，而偏相关函数呈现截尾，故可对该序列拟合 AR（p）模型。

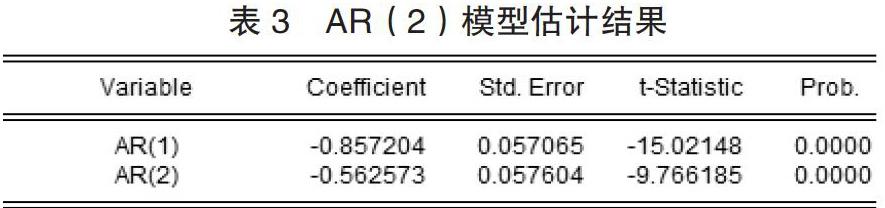
根据 SIC 和 SBC 最小原则选择模型的最佳阶数，应该选择 AR（2）模型，其 SIC 值为-6.0298、SBC 值为-5.998。

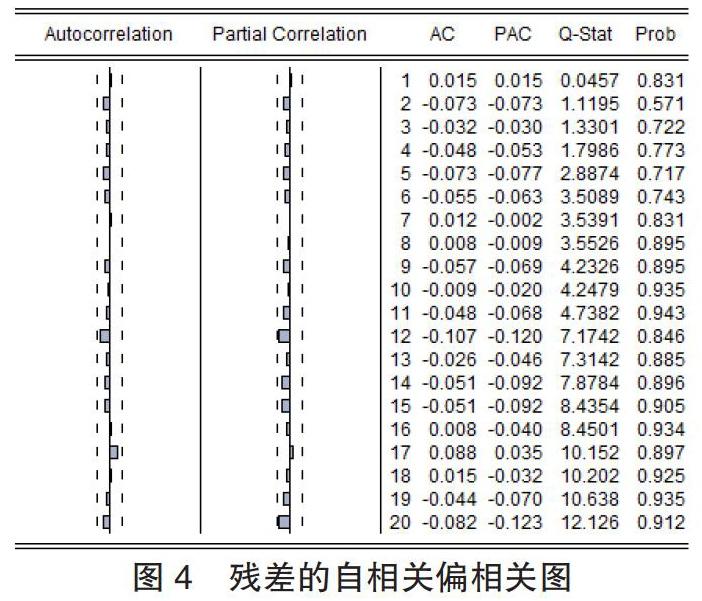
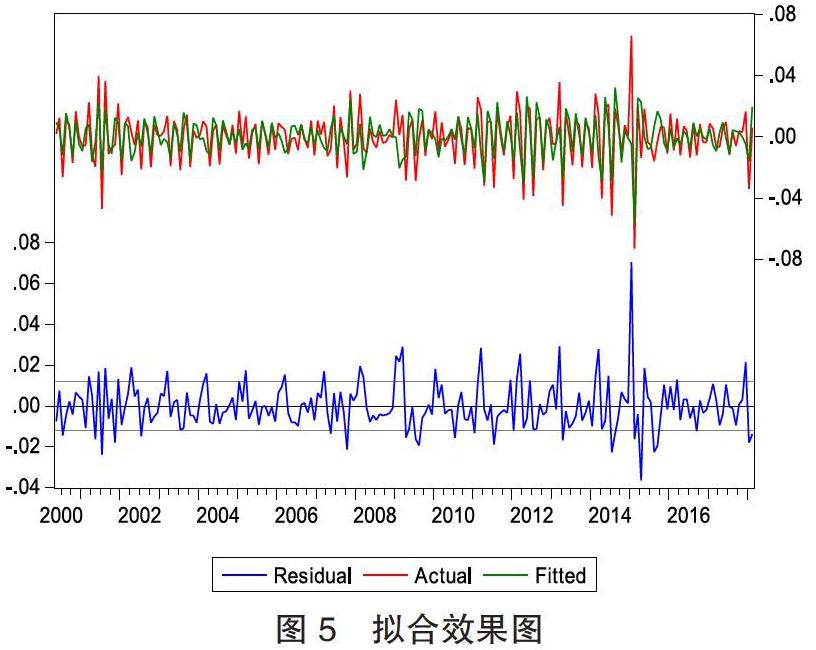
由 AR（2）模型估计结果残差的自相关偏相关图 4 可知残差序列为白噪声。将原始序列和经过模型预测出来的序列进行对比（见图 5），可以说明模型拟合效果较好。

（四）结果分析及预测

1.OLS 结果分析。回归模型经过估计检验后，由 t 检验知系数显着，由可决系数为 0.99413 可见拟合效果很好，可以求得拟合方程如下：ln（y）=11.6159+0.013281t+εt，根据拟合方程预测出 t=219 时 ln（y）=14.52，其同比增长率为 1.33%，远大于实际情况下 t=218 时的同比增长率-0.42%，因而该预测结果的准确性和合理性存疑。

2.ARMA 结果分析。由上述研究可得出 AR（2）模型方程为：

由此可以预测得到 t=219 时 ln（y）=14.27，同比增长率为-0.013%，相对较接近实际情况下 t=218 时的同比增长率-0.42%，故该预测结果比较合理准确，即预测出 2018 年 3 月我国金融机构存款为 1696108.696 亿元。

四、结论

由前面的预测结果可知，相对于常规的 OLS 模型，ARMA 模型能够较为准确、合理地对我国金融机构各项存款总和进行短期预测，这对国家根据宏观货币管理的需要，以及维持金融机构资产流动性的需要，合理进行货币政策的调整，引导商业银行等金融机构交存中央银行存款准备金的比率和结构，借以间接地对社会货币供应量进行必要的调控具有重要的参考价值。

参考文献：

[1]邱洪涛.互联网理财产品对地方法人金融机构存款冲击的分析——以周口市为例[J].时代金融，2014（29）：252-253.

[2]胥红.银行单位活期存款快速增加值得关注——对常德市银行业金融机构单位活期存款的调查与分析[J].金融经济，2017（06）：83-84.

[3]闫静文，张晋伟.经济下行背景下资源型经济存款增速下滑的调查与思考——以山西省为例[J].经济师，2015（06）：117+119.

[4]Rui Han，Martin Melecky. Broader Use of Saving Products Among People Can Make Deposit Funding of the Banking System More Resilient[J]. Journal of International Financial Markets， Institutions & Money，2016.

[5]徐煜程.基于 ARMA 模型对我国金融机构存款的分析[J].中国集体经济，2017（08）：77-78.

作者单位：云南师范大学经济与管理学院；邹泉为本文通讯作者

作者张会荣邹泉