基于主成分分析的股票多因子量化投资策略研究

摘要：本文利用中国 A 股市场中所有股票近年来的相关财务数据与行情数据，对 500 多个股票因子进行了显着性分析与主成分分析，构建了两个新的选股主因子：技术因子与价值因子，并以此为基础建立了多因子量化选股策略。最后利用近五年数据对该策略进行了回测与实证分析，结果表明该策略在不同市场行情下都能够在低风险的同时稳定地获取超过基准收益率的高额回报。

关键词：量化投资 股票 主成分分析 多因子模型

一、引言

Famma 与 French（1993）[1]基于市值、账面市值比和市盈率建立了着名的三因子模型，奠定了多因子选股模型的理论基础。目前，人们已经提出了上千种能够反应股票各种信息的因子，因而如何从中选取符合市场行情的有效因子成为了当下热点研究问题之一。而主成分分析方法[2] [3][4]可以很好地解决这一问题，其不仅可以提炼出对股票收益率有显着影响的因子，并且可以解决各因子数据间的相关性问题。

二、数据预处理

本文以中国 A 股市场中的全部 3000 余只股票和点宽网因子库中的所有 500 多个因子作为研究对象，数据来源于点宽网的商用数据库，研究的样本区间为 2016 年 1 月 1 日至 2018 年 9 月 30 日。所使用的数据分析软件和编程软件为 SPSS、AutoTrader 与 MATLAB。

首先根据准则对数据进行去极值处理，然后采用零均值化，将数据按照一定比例缩放到 0 与 1 之间，并满足均值为 0、标准差为 1，最终得到标准化的数据。记为因子库中的全部因子，为 A 股市场中的全部股票，其中 N、M 分别表示因子的总个数和股票的总只数。用序列表示股票对应于因子的日频数据，其中为样本区间内总交易天数。

由于某些因子值需要根据各公司月度财报数据进行更新，因而本文的模型均采用按月换仓的交易策略，这就需要将前文的日频数据序列转化为月度数据序列。设整个样本区间共包含了 T 个月，用序列表示股票 Si 对应于因子 Xj 的月度数据，其中取为中第 t 个月的最后一个交易日所对应的数值。

三、IC 显着性分析

IC（信息系数）是由因子在某只股票上的因子暴露与对应股票下一期收益序列间的相关系数来确定的，即因子 Xj 关于股票 Si 的 IC 值为

其中为因子月度数据序列的前 T-1 个分量，而为股票 Si 的每期收益率序列，其中每期的收益率为

可见 IC 值的绝对值越大股票收益率就越高，故使用 IC 值的绝对值去判断因子与股票收益之间的关系。由此定义每个因子针对全市场所有股票的 IC 显着性为

显着性越大表明该因子与股票价格之间的相关性就越高，则其对股价的预测能力就越强。通过计算因子库中 500 多个因子的 IC 显着性，本文筛选出最优的 20 个候选因子（见表 1）。

对于 IC 显着性大的因子还需要进一步考察其选股能力的实际表现，即观察因子值高的股票是否能够保持盈利。为此本文建立了单因子选股模型（详见模型 1），并利用样本区间的真实市场数据，对表 2 中的因子逐一进行回测分析。

模型 1 单因子选股模型

1.手续费为双边 3‰，每月月初调仓。

2.在每月最后一个交易日计算股票的因子得分。

3.分值最大的前 3% 的股票作为备选股票池。

4.在下月首个交易日，以当天的收盘价将持仓股票更换为备选股票池中股票。

5.对历史收益率进行回测并计算夏普比率。

其中第 2 步的因子得分是通过对原始数据进行预处理之后得到的一个数值（详见算法 1）。

算法 1 计算单只股票的因子得分

1.提取之前 30 个交易日的原始因子数据。

2.按照第一节的方法进行去极值与标准化处理。

3.以最后一个交易日对应的数值作为因子得分。

由于夏普比率能够同时反映出投资的收益与风险，故本文以此作为度量选股能力的指标，并据此选取夏普比率最高的前 6 个因子作为最终的有效因子，分别记为 Y1，…，Y6（见表 2）。

四、主成分分析及多因子选股模型

为防止不同因子之间存在内在关联而导致信息重叠，本文利用样本区间内的月度数据对上述有效因子进行主成分分析。

其次，利用 SPSS 对于矩阵 A 进行主成分分析，得到了表 3 所示的主成分方差贡献累积和特征值。

由于前两个成分的累积方差贡献率达到了 87.291%，已经能够涵盖的绝大部分的信息量，因而选择 F1，F2 作为主成分，其关于 Y1，...，Y6 的组成系数分别为：

如果两个主成分对因子的影响程度相似，则这两个主成分是很难区分的，为此需要进行适当的坐标旋转，将其换成新的主成分。记，观察发现 V 的前三行和后三行分别对应平面上两类不同的点。因而构造二阶正交旋转矩阵 S，对 V 进行旋转变换得到，其中为 W 的列向量，且满足分别只在前三行和后三行的位置上取值最显着，容易解得：

通过中各分量取值的权重可以看出，与三个价值类因子 NegMktValue、MktValue、LFL 密切相关，其所包含的信息主要为公司的基本面信息，因此称为价值因子。而与三个技术指标类因子 LINEARREG_INTERCEPT、HT_TRENDLINE、KAMA 密切相关，其所包含的信息主要为股票行情 K 线的基本数据，因此称为技术因子。

将价值因子与技术因子的值进行等权重相加，作为衡量股票优劣性的指标，由此建立如下多因子量化选股模型（详见模型 2）。

模型 2 多因子量化选股模型

1.手续费为双边 3‰，每月月初调仓。

2.在每月最后一个交易日，根据算法 1 计算股票关于有效因子的因子得分。

3.计算出合成因子的值，并以作为该股票的综合得分。

4.取分值最大的 3% 的股票作为备选股票池。

5.在下个月的首个交易日，以当天的收盘价将持仓股票更换为备选股票池中股票（根据不同股票价格等权重配置资金）。

6.对历史收益率进行回测，计算其年化收益率、夏普比率与最大回撤等相关指标。

五、实证分析

从整体上来观察上证 50 指数自 2014 年 5 月至今的走势（见图 1），可以清晰地看出大盘经历了从大涨到大跌、最后进入一个缓慢盘整的过程。

因而可以将整个时间段分为 3 个不同走势的部分，即「牛市」「熊市」「震荡市」，其具体时间分段如下：

a）牛市：14 年 5 月 1 日至 15 年 5 月 31 日。

b）熊市：15 年 6 月 1 日至 16 年 4 月 30 日。

c）震荡市：16 年 5 月 1 日至 19 年 6 月 30 日。

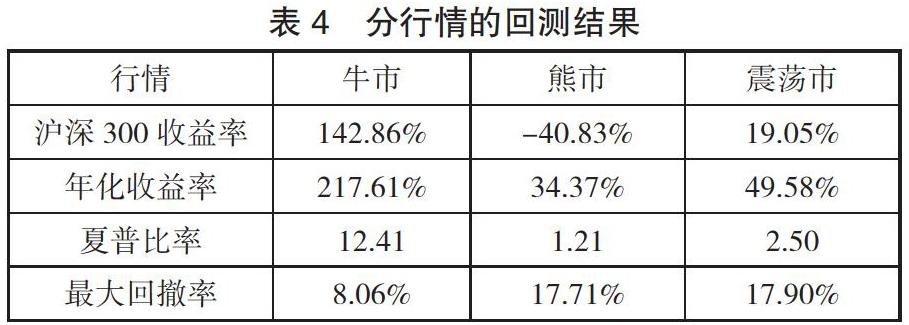
将模型 2 分别在这三个时间段上进行回测，结果如下表所示。

由表 4 可知，该模型在不同行情下的年化收益率都显着优于同期沪深 300 指数的收益率。在牛市行情当中，该模型取得了较高的夏普比率和较低的最大回撤率，表明该模型不仅能够获取非常稳定的高额收益，而且具有非常低的投资风险。在熊市和震荡市期间，该模型受行情影响较大，从而导致了收益率与夏普比率的下降以及最大回撤率的上升，但相对于沪深 300 指数而言，仍然具有明显的投资优势。

总之，模型 2 能够很好地适应各种市场行情，不仅获得了超过市场平均水准的收益，而且也完全体现出了低风险性。进而也说明了本文所构造的价值因子与技术因子，在各种行情下都能够较为准确地反应出股票的优劣性。

参考文献：

[1]E Fama，K French. Common Risk Factors in the Returns on Stocks and Bonds[J].Journal of Financial Economics，1993，33（3）：3-56.

[2]朱晨曦.我国 A 股市场多因子量化选股模型实证分析[D].北京：首都经济贸易大学，2017.

[3]王春丽.刘光.王齐.多因子量化选股模型与择时策略[J].东北财经大学学报，2018，（5）：81-87.

[4]于卓熙.秦璐.赵志文.温馨.基于主成分分析与广义回归神经网络的股票价格预测[J].统计与决策，2018，510（18）：168-171.

基金项目：北京师范大学珠海校区教师科研能力促进计划项目。

作者单位：北京师范大学珠海校区应用数学学院

作者 丁琦