我国宏观经济指数的构建与预测

摘要：预测我国经济未来发展趋势对维护我国经济的持续发展具有重要意义，本文选取了 9 个反映宏观经济的相关指标，利用主成分分析法构建我国宏观经济指数。同时，基于灰色系统理论，建立 GM（1，1）模型对宏观经济指数进行拟合及预测。结果表明，我国宏观经济指数总体呈持续上升趋势，2008 年以前指数较低，之后保持较高水平。此外，预测结果表明宏观经济指数在 2019 年和 2020 年会继续保持上升趋势。

关键词：宏观经济  主成分分析  灰色系统理论  GM（1，1）模型

一、引言及文献综述

当前世界各国之间的竞争日益激烈，国家的经济实力是其国际竞争力的核心要素之一，国家的宏观经济水平是衡量一国经济发展的重要依据，宏观经济的稳定发展对提升国家的国际竞争力具有非常重要的意义。

关于指标体系的评价研究，学者们提供了不同的思路。比如郭金花等采用熵值法构建了文化产业融合创新能力评价指标体系，并对我国 31 个省份的文化产业融合创新能力进行综合评价与差异分析[1]。但更多学者运用主成分分析法构建指标体系并进行综合评价，如刘晓星等运用了主成分分析方法，构建了覆盖银行业、保险业、证券业等三大金融部门的金融监管综合评价指数[2]。郭建民等从规模、效益、增速、产能结构、创新能力与产业竞争力等六个维度选取指标，运用主成分分析法对国际产能合作评价指标进行综合评价[3]。而针对数据预测，学者们的研究思路十分广泛。赵洪科等利用深度神经网络，对互联网金融市场的日交易量和日交易次数进行预测[4]。修静等构建绿色信贷、节能减排下的工业增长模型，运用更为成熟的灰色系统模型，预测了我国至 2020 年的工业增长路径[5]。

本文主要围绕我国宏观经济指数的构建与预测进行，采用较为成熟的主成分分析法，选取 9 个宏观经济指标，构建我国的宏观经济指数。并在此基础上，根据灰色系统理论，建立 GM（1，1）模型对宏观经济指数进行拟合及预测。

二、指标与数据来源

在参考众多学者的研究基础上，本文选取 1998 年第 1 季度至 2018 年第 4 季度的相关指标构建我国宏观经济指数，包括外汇储备、储蓄存款、国内生产总值、M2、实际汇率指数、存贷比、失业率、不良贷款率、消费者信心指数。本文选取的指标数据来源国家统计局、Wind 数据库、CEIC 数据库等。

三、模型介绍

主成分分析是将多变量之间的复杂关系进行简化处理的常用方法，将较高线性相关性的高维变量降维成线性无关的低维变量，从而可以保证在数据信息丢失最少的前提下，将数据进行综合简化，降低进一步分析的难度。本文采用 GM（1，1）模型对宏观经济指数进行拟合和预测，GM（1，1）预测模型的建立步骤如下：

首先，获得原始数据的序列。其次，利用累加方法，弱化原始数据的随机性，构造生成序列，其中。之后，建立对应 GM（1，1）模型的微分方程形式：

四、实证分析

（一）宏观经济指数与 GM（1，1）模型构建

图 1 显示了利用主成分分析法构建的 1998 年-2018 年各季度的我国宏观经济指数的变化情况，宏观经济指数呈现出较为明显的上升趋势，但是 2012 年以前的宏观经济指数整体水平较低。鉴于二十年来中国经济整体形势不断发生变化，灰色预测模型也适用于较为短期的序列的处理，因此本文选取了 2012 年第一季度到 2018 年第四季度的宏观经济指数作为原始数据用于拟合及预测。

经计算，发展灰数，内生控制灰数，预测模型为，根据得到的拟合的生成序列累减得到拟合序列，拟合序列如表 1 所示。

（二）有效性检验

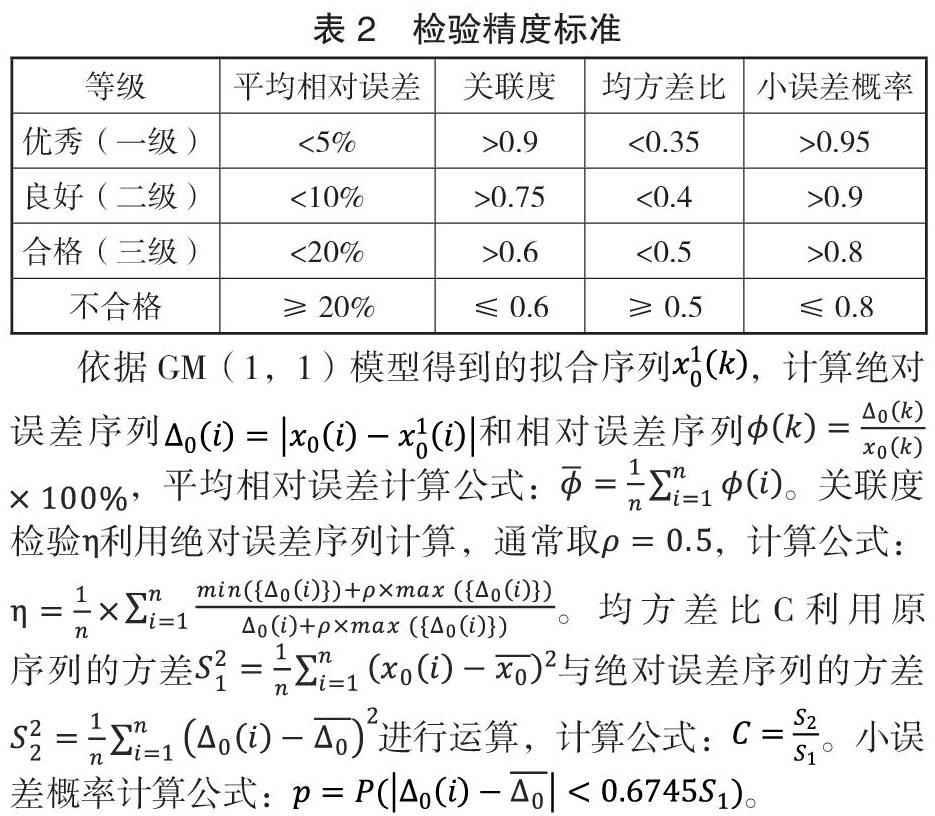
GM（1，1）的拟合结果需要经过检验以确保模型预测的有效性。GM（1，1）模型的检验方法包括残差检验、关联度检验、均方差比检验、小误差概率检验。各检验的精度标准如表 2 所示。

依据 GM（1，1）模型得到的拟合序列，计算绝对误差序列和相对误差序列，平均相对误差计算公式：。关联度检验利用绝对误差序列计算，通常取，计算公式：。均方差比 C 利用原序列的方差与绝对误差序列的方差进行运算，计算公式：。小误差概率计算公式：。

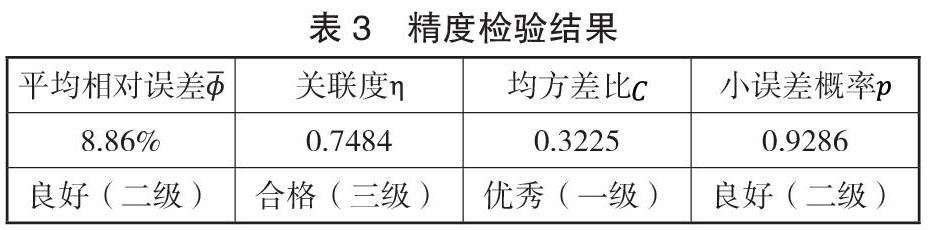
经计算，本文的模型计算得到的结果的精度检验结果如表 3 所示。拟合结果通过残差检验、关联度检验、均方差比、小误差概率检验，因此可以对未来的我国宏观经济指数进行预测。

（三）预测结果

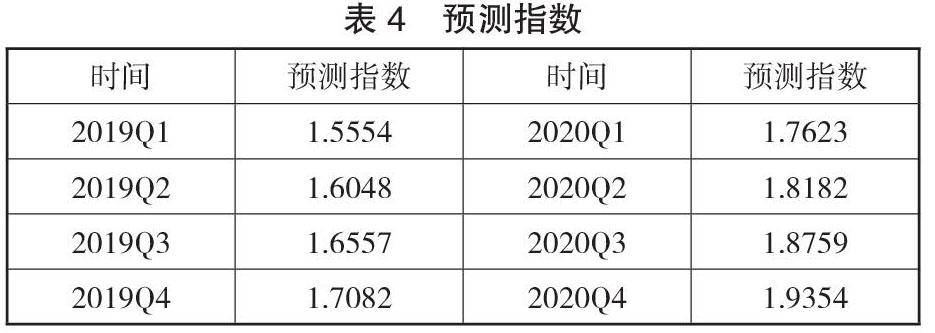
利用计算得到的 GM（1，1）对 2019 年及 2020 年的我国的宏观经济指数进行预测，预测结果如表 4 所示。从预测结果可以看出，我国的宏观经济指数在 2019 年和 2020 年将平稳增长。

五、结论

本文选取 1998 年第一季度至 2018 年第四季度的相关指标数据，利用主成分分析的方法，构建了我国的宏观经济指数。建立 GM（1，1）模型对宏观经济指数进行拟合及预测，该模型通过了有效性检验，并具有较高的精度。运用该模型对我国 2019 年至 2020 年的宏观经济指数进行预测，结果显示我国宏观经济指数将继续保持平稳增长态势。基于以上结论，提出相关建议，长期而言我国经济稳中向好的基本面并没有发生改变，但随着我国经济进入新常态、国际经济环境复杂多变，我国经济在短期内面临的内外部挑战依旧存在。应当注重化解风险，维护我国经济平稳发展。

参考文献：

[1]郭金花，郭淑芬.文化产业融合创新能力评价指标体系构建与测评[J].统计与决策，2019，35（12）：62-65.

[2]刘晓星，赵鹏飞，卢菲.全球化条件下金融监管指数构建及其国际比较[J].江苏社会科学，2014（1）.

[3]郭建民，郑憩.开展国际产能合作评价指标体系及实证研究[J].宏观经济研究，2019（09）：80-87+101.

[4]赵洪科，吴李康，李征，张兮，刘淇，陈恩红.基于深度神经网络结构的互联网金融市场动态预测[J].计算机研究与发展，2019，56（08）：1621-1631.

[5]修静，刘海英，臧晓强.绿色信贷、节能减排下的工业增长及预测研究[J].当代经济科学，2015，37（03）：55-62+126.

作者单位：东南大学经济管理学院

作者 李经纬 朱冬冬