期权波动率定义的理论错误及纠正
 作者
作者



摘要:本文指出了期权定价理论将股票价格假设为随机变量的数学抽象错误,以及使用描述大量样本轨道偏离均值离散程度的标准差来度量一条样本轨道波动程度的基本概念错误。本文依据股票价格与时间「一一对应」的数量关系,将股票价格抽象为随机过程中的一条样本轨道,并用刻画时间函数在某一区间相对变化程度的相对变化率来度量股票价格波动程度,可真实反映股票价格的波动程度、收益率及风险大小,为量化分析、投资决策、资产定价和风险管理提供有效可靠的科学依据和分析工具。
关键词:股票价格;波动率;风险度量
一、引言
波动率(Volatility)是期权定价理论度量金融资产价格波动程度的一个统计参数。准确度量并预测股票价格的波动程度,不仅可为证券投资活动的量化分析、投资决策、资产定价、最优配置、风险管理及市场监管提供有效可靠的科学依据,而且对于完善股票市场的监管措施、防范和化解股票市场的系统性风险、减小股票市场对社会经济造成的影响,促进社会经济的持续稳定发展具有重要意义。由于随机过程定义及基本概念的抽象性和复杂性,期权定价理论将股票价格与时间之间的数量关系错误地抽象为随机变量,并根据众多学者「股票价格的短期对数收益率为白噪声序列」的实证研究结果,建立了描述股票价格波动现象的几何布朗运动模型,得出了股票价格服从对数正态分布的结论,因而用刻画正态分布随机变量与其均值偏离程度的标准差来度量股票价格的波动程度。
期权定价理论将股票价格与时间之间的数量关系抽象为随机变量,无形中使研究对象从一条样本轨道改变为大量样本轨道的集合,并用描述大量样本轨道偏离均值离散程度的统计参数(标准差)来度量一条样本轨道的波动程度,因而无法正确度量股票价格的波动程度。本文依据股票价格与时间「一一对应」的数量关系,将股票价格抽象为随机过程中的一条样本轨道,并用刻画时间函数在某一区间相对变化程度的相对变化率来度量股票价格波动程度,可同时度量股票价格的波动程度、收益率及风险大小。
二、布朗运动理论
1827 年,英国植物学家布朗使用显微镜观察悬浮在液体中的花粉微粒时,发现微粒总是在做无规则的运动。后来人们发现,这是一种广泛存在于自然界、工程技术和人类社会中的动态随机现象,如空气污染扩散、陀螺随机游走和股票价格波动等。
1905 年,爱因斯坦首先使用概率分析方法对布朗运动进行了定量研究,为统计热力学和随机过程基础理论的发展奠定了基础。爱因斯坦认为布朗运动是由大量液体水分子的连续碰撞造成的,并从热分子运动扩散方程推导出了大量一维布朗粒子的位置 x 在 t 时刻的概率密度函数(张太荣,2008):
式中 D 为扩散系数,是物理学刻画物质扩散速度的物理量,量纲为 m2/s。
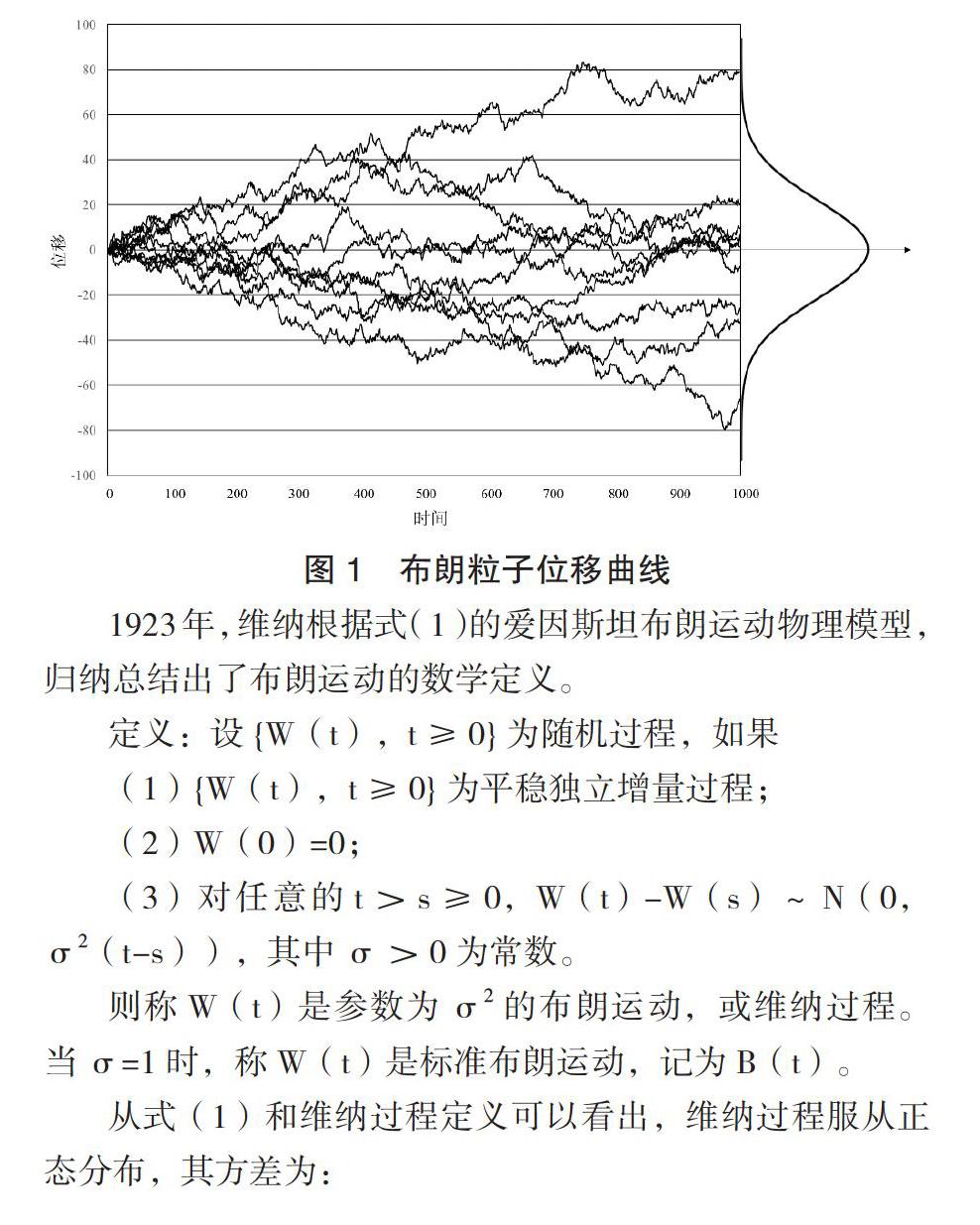
式(1)表明,大量布朗粒子在 t 时刻的空间位置服从参数为(0,2Dt)的正态分布,图 1 给出了 10 个布朗粒子的位移曲线,可以看出,每个布朗粒子的位移均是时间 t 的函数。
1923 年,维纳根据式(1)的爱因斯坦布朗运动物理模型,归纳总结出了布朗运动的数学定义。
定义:设{W(t),t≥0}为随机过程,如果
(1){W(t),t≥0}为平稳独立增量过程;
(2)W(0)=0;
(3)对任意的 t>s≥0,W(t)-W(s)~N(0,σ2(t-s)),其中 σ>0 为常数。
则称 W(t)是参数为 σ2 的布朗运动,或维纳过程。当 σ=1 时,称 W(t)是标准布朗运动,记为 B(t)。
从式(1)和维纳过程定义可以看出,维纳过程服从正态分布,其方差为:
D[W(t)]=σ2=2Dt;; (2)
维纳过程的方差 σ2 是用来刻画随机变量偏离均值分散程度的数字特征,度量的是大量样本轨道偏离均值的发散程度,其物理意义与表示大量布朗粒子偏离原点扩散速度的扩散系数 D 相同。
标准差 σ 不仅能度量服从正态分布的随机变量偏离均值的发散程度,还能给出随机变量位于 ±σ、±2σ 和 ±3σ 范围内的概率分别为 68.3%、95.4% 和 99.7%。
维纳过程的定义及性质是以随机变量的形式给出的,不能直接用来描述单个布朗粒子位移随时间演变的过程,导致自然科学、工程技术和社会科学在研究动态随机现象时,将单个布朗粒子位移、光纤陀螺随机游走误差和金融资产价格错误地抽象为随机变量,并用刻画随机变量偏离均值离散程度的标准差来描述一条样本轨道的时间运动规律,从而得出了一系列与事实不符的错误结论。例如,人们根据「维纳过程方差与时间成正比」的结论,竟得出了下面的单个布朗粒子位移公式:
x(t)=; (3)
式(3)表明,单个布朗粒子的位移与时间的平方根成正比,与牛顿力学「质点位移与时间成正比」的结论不一致。
高宏(2019)从随机过程样本轨道角度重新定义了维纳过程,给出了维纳过程样本轨道的位移公式、自相关函数和功率谱密度,得出了与牛顿力学「质点位移与时间成正比」完全一致的结论,可直接用于描述自然科学、工程技术和社会科学中的随机运动现象、特性及规律。
三、股票价格与时间之间的数量关系
观察股票价格随时间的变化过程,有时间 t 和股票价格 s 两个变量,这两个变量并不是孤立地变化,股票价格 s 随时间 t 的变化而变化。设 s(t)为 t 时刻的股票价格,则对于任一个时间值 t,股票价格都有唯一确定的值 s(t)与 t 对应,两者之间存在着「一一对应」的函数关系,因此,股票价格 s (t)无疑是时间 t 的函数。
但是,期权定价理论却将实际股票价格 s(t)抽象为随机变量 S(t),股票价格究竟是时间函数 s(t)?还是随机变量 S(t)?
我们以标准布朗运动为例,分析随机过程、随机变量和样本函数三者之间的区别与关系。随机过程 B(t)实质上是定义在参数集 T 和状态空间 Ω 上的二元函数 B(ω,t)。对于固定的时间 t,B(ω,t)为状态变量 ω 的函数,称为随机变量,通常简记为 B(t);对于固定的 ω,B(ω,t)为时间 t 的函数,称为样本函数或样本轨道,简记为 b(t)。因此,随机过程即可看成是大量随机变量 B(t)的集合,也可看成是所有样本轨道 b(t)的集合,所有样本轨道 b(t)在 t 时刻的取值就是随机变量 B(t)在 t 时刻的状态。随机变量 B(t)用来描述大量布朗粒子在 t 时刻的空间位置分布状态,随机变量的标准差 σ 可用来度量大量布朗粒子偏离原点的扩散程度,样本函数 b(t)则用来描述单个布朗粒子位移随时间的演变过程。
注意:B(t)并不表示 B(t)是时间 t 的函数,它只表示随机变量 B(t)在 t 时刻的状态。
图 1 所示的布朗粒子位移曲线清楚地表示出了随机过程、随机变量和样本函数三者之间的关系。每个布朗粒子的位移曲线就是随机过程定义中的样本函数 b(t),10 个布朗粒子的位移曲线(10 条样本轨道)就构成了随机过程 B(t),所有样本轨道 b(t)在 t 时刻的取值就是随机变量 B(t)在 t 时刻的状态。因此,随机变量 B(t)和样本函数 b(t)描述的是完全不同的物理现象,随机变量 B(t)用来描述大量布朗粒子在 t 时刻的空间位置分布,样本函数 b(t)用来描述一个布朗粒子随时间的运动过程。
一个样本函数或一条样本轨道对应着随机试验中的一次「测量结果」,尽管每个布朗粒子的位移测量结果各不相同,但是单个布朗粒子的测量结果却是一个确定性的时间函数。
股票价格的变化过程 s(t)与一个布朗粒子位移的变化过程 b(t)在数学形式上完全相同,根据随机过程的定义,股票价格 s(t)只能被抽象为随机过程中的一条样本轨道,而非随机变量 S(t)。
四、几何布朗运动模型
众多学者通过对股票价格波动现象长期观察和实证研究,发现股票价格的变化是完全随机的,股票价格的短期对数收益率为零均值不相关白噪声序列。
设 s(t)为 t 时刻的股票价格,y(t)=ln s(t),则股票价格 s(t)的对数收益率(日)可表示为:
y(t)- y(t-Δt)=x(t)(4)
式中 x(t)为白噪声函数,不同时刻的 x(t)值服从均值为零、标准差为 σt 的正态分布。
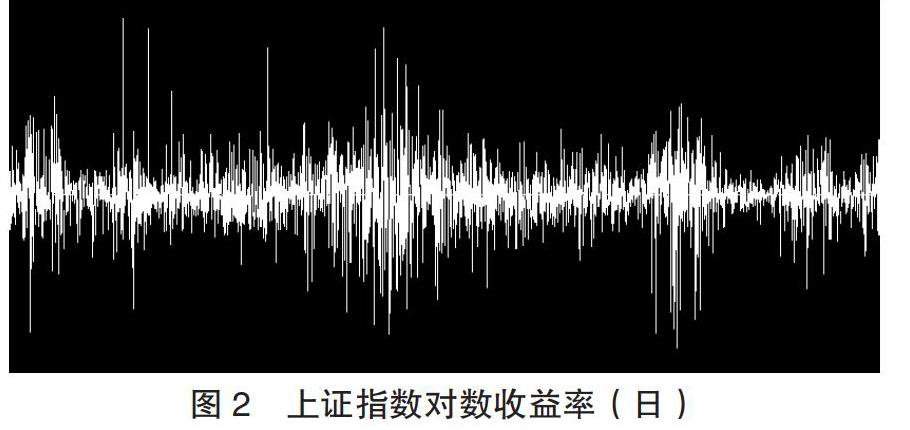
图 2 为上证指数 1998 年-2020 年的收盘价对数收益率(日),可以看出,上证指数的对数收益率为白噪声序列,在下一时刻的方向和大小完全随机变化。将不同时刻的上证指数对数收益率作为样本点进行统计分析,其均值为 0.0002,标准差 σt=0.02,最大波动幅度为 0.09,近似服从正态分布,有明显的尖峰厚尾现象。
由于时间间隔 Δt 很小,短期对数收益率与百分比收益率近似相等,式(4)可改写为:
(5)
式中 b(t)为标准布朗运动 B(t)的样本函数,b(t)的一阶差分 Δb(t)为服从(0,1)正态分布的白噪声。
式(4)和式(5)中的 y(t)、x(t)、s(t)和 b(t)均为时间函数,但是期权定价理论却将他们抽象为随机变量 Y(t)、X(t)、S(t)和 B(t),于是式(4)和式(5)分别变化为:
Y(t)=Y(t-Δt)+X(t)(6)
(7)
X(t)为各态历经随机过程,其样本函数 x(t)的时间平均与随机变量 X(t)的统计平均在概率意义上相等,因此 X(t)的方差为:
(8)
即 X(t)为服从(0,σ2)正态分布的高斯白噪声随机过程。
设 Y(0)=0,则 Y(t)的数学期望和方差分别为:
E[Y(t)]=0;(9)
D[ Y(t)]= σ2t (10)
式(9)和式(10)表明,对数股票价格 Y(t)服从参数为(0,σ2t)的正态分布。
Y(t)的数学期望为零,与实际股票价格中存在长期线性趋势的事实完全不符,为了使式(6)和式(7)能够描述长期线性趋势,Samuelson 增加了线性漂移项,建立了下面的股票价格数学模型:
Y(t)=μt+Y(t-Δt)+X(t)(11)
(12)
式中 μ 为漂移率,是指单位时间内股票价格对数收益率或百分比收益率均值的变化值。
式(11)称为随机游走模型,式(12)称为几何布朗运动模型,两者的短期对数收益率始终为 μ,与「股票价格短期对数收益率为零均值不相关白噪声」的实证研究结果不符。
求解式(12)微分方程:
(13)
因此对数股票价格 ln S(t)的数学期望和方差分别为:
(14)
(15)
表明 ln S(t)服从方差为 σ2t 的正态分布(Hull,2011)。
正态分布的 ln S(t)曲线应具有正态分布的对称性和集中性,但实际对数股票价格 ln s(t)曲线完全不满足正态分布的对称性和集中性。
从上面的几何布朗运动模型建立过程可以看出,式(12)的股票价格几何布朗运动模型存在下述 2 个严重错误:
第一,股票价格 s(t)是时间 t 的函数,随机游走模型和几何布朗运动模型却将其假设为随机变量 S(t),无形中将研究对象从一个样本函数改变为大量样本函数的集合。
第二,实际对数股票价格曲线不具有正态分布的对称性和集中性,股票价格服从对数正态分布的结论与事实不符。事实上,几何布朗运动模型描述的是图 1 所示的大量样本轨道(漂移率 μ=0)在状态空间的正态分布情况,而不是一条样本轨道随时间的演变过程。
五、股票价格线性趋势和波动范围
式(4)和式(5)是众多学者通过对股票市场长期观察和实证研究得到的经验模型,也是对未来股票价格运动现象所做出的一种假定性和推测性论断。因此式(4)和式(5)是建立期权定价理论或推导其他命题的起点和基础。从式(4)和式(5)经严格逻辑推理得到的相关命题和结论,对股票价格具有解释和预见功能,能够预测股票价格的发展趋势和变化结果。
将式(4)看作股票对数价格 y(t)的一阶差分,设 y(0)=0,则有:
(16)
将其变换为:
(17)
式中为白噪声函数 x(t)在区间[0,t]上的算数平均值,其物理意义为白噪声函数在区间[0,t]被截断后,因「频谱泄露」效应而产生的直流分量。
也是一条随机过程样本轨道,由概率论大数定律可知,随着 t 的增加,的时间均值 会趋于一个常数,设 E[]= μ,则 y(t)中存在一条 μ t 的长期线性趋势线。
从信号分析的角度看,对白噪声信号 x(t)进行算数平均,相当于对 x(t)进行低通滤波,使 x(t)中的高频分量被衰减,低频分量被放大,因此,是一个围绕均值 μ 缓慢波动的低频信号。
算数平均值的方差为:
(18)
式中 σt 为白噪声函数 x(t)的标准差。
反应了围绕 = μ 上下波动的程度,在 μ±3 范围内波动的概率为 99.73%。当 t 较小时,变化异常剧烈,y(t)表现出很强的随机性;当 t 充分大时,趋于稳定,y(t)围绕长期线性趋势线 μ t,在固定宽度的线性通道内缓慢波动上行。
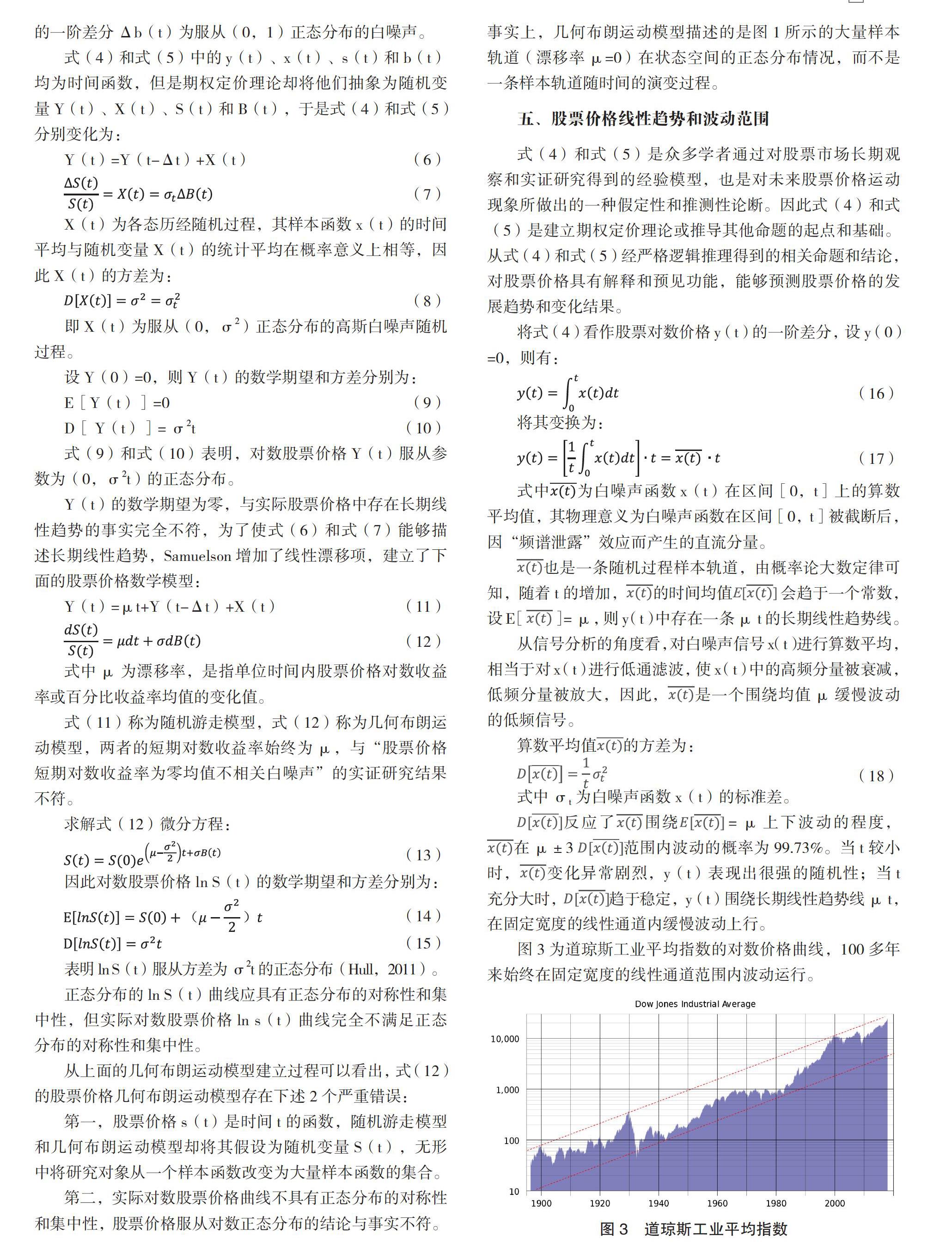
图 3 为道琼斯工业平均指数的对数价格曲线,100 多年来始终在固定宽度的线性通道范围内波动运行。
六、波动率定义错误
期权定价理论假设资产价格服从对数正态分布(Augen,2016),并用一年内的股票连续复利收益率的标准差来定义股票价格的波动率(Natenberg,2019)。
由式(15)的方差计算公式,可直接写出期权到期时间 T 时的波动率 σT 计算公式:
(19)
式中 T 为期权到期时间,σ 为股票价格几何布朗运动模型参数,即式(8)定义的随机变量标准差,σ 在概率意义上等于股票日对数收益率的标准差 σt。
(一)波动率的物理意义
将对数股票价格 y(t)视为一个布朗粒子在 t 时刻的位移,则 y(t)与布朗粒子运动的数学模型完全相同,即 y(t)的一阶差分 Δy(t)和布朗粒子位移的一阶差分均为白噪声函数 x(t)。对数股票价格 y(t)曲线就相当于图 1 中的一个布朗粒子位移曲线(一条样本轨道)。
波动率(标准差)与扩散系数 D 具有相同的物理意义,是描述大量布朗粒子扩散速度的统计参数和物理量,不能用来度量一个布朗粒子位移的波动程度。
从随机过程的角度看,标准差是度量大量样本轨道偏离均值离散程度的统计参数,无法用来描述一条样本轨道的波动程度。
(二)波动范围与事实不符
期权定价理论假设股票价格服从式(12)几何布朗运动模型描述的对数正态分布,则 t 时刻对数股票价格 y(t)的方差为 σ2t,因此,y(t)在范围内波动的概率为 99.73%,这表明对数股票价格 y(t)的波动范围会随时间 t 的平方根不断增大,与实际对数股票价格在固定宽度的线性通道内运行的观察结果(见图 3)严重不符。
(三)数学抽象错误
将实际问题正确地抽象为数学问题是建立科学理论或解决实际问题的第一步,也是最为关键和重要的一步。如果不能将实际问题正确地抽象为数学问题,即使使用正确的数学推理和分析方法,也会得出一系列错误的结论。
前面已经对股票价格与时间之间的数量关系进行了分析,得出股票价格是时间函数的结论。根据随机过程定义,股票价格只能被抽象为随机过程中的一条样本轨道 s(t),而非随机变量 S(t)。
期权定价理论错误地将实际股票价格 s(t)抽象为随机变量 S(t),无形中使研究对象从一条样本轨道改变为大量样本轨道的集合,导致整个期权定价理论建立在错误的随机变量假设基础上,并使用描述大量样本轨道扩散速度的统计参数(标准差)来度量一条样本轨道的波动程度,必然无法正确描述、解释和预测股票价格波动现象及规律,在实际应用时给金融市场带来巨大的灾难。
(四)正态假设与事实不符
期权定价理论首先假设资产价格服从对数正态分布,然后用正态分布的标准差来度量资产价格偏离平均值的程度。
图 2 为上证指数的日收益率。上证指数的日收益率在下一时刻的正负和大小是完全随机的,将不同时刻的上证指数日收益率作为样本点进行统计分析,上证指数的日收益率分布曲线是一条中间高,两端逐渐下降且完全对称的钟形曲线,与正态分布近似,并具有如下的正态分布性质:
1.对称性。绝对值相等的正、负收益率出现的次数大致相等。
2.集中性。收益率分布曲线的高峰位于正中央。
图 4 为上证指数自 2003 年 9 月至 2020 年 9 月的年收益率曲线。上证指数的年收益率曲线在一段时间内始终上升,在另一段时间内一直下降。也就是说,上证指数的年收益率不是完全随机变化,而是存在明显的确定性变化趋势,不具有正态分布的对称性和集中性,不满足期权定价理论的正态分布要求,因此,日收益率的标准差根本无法用来度量图 4 所示年收益率的波动程度。
(五)风险度量问题
期权定价理论将方差作为风险的度量,由于不考虑价格变动的方向,因此偏离了投资风险的原始含义。
投资风险的原始含义是指遭受损失的可能性。股票价格向上波动会给投资者带来收益,向下波动才会给投资者造成损失。如果将股票价格向上的大幅波动视为风险,投资者在规避风险的同时,也会失去获取超额收益的良好机会。因此,波动率在理论和实践上均无法真实反映投资风险的本质,与投资者的心理感受完全不一致。
(六)模型参数错误
式(12)的几何布朗运动模型是随机微分方程,其参数在概率意义上等于股票价格日收益率的标准差,但是期权定价理论却将股票价格的年波动率当作几何布朗运动模型和 BS 期权定价公式中的使用(Hull,2011)。
七、重新定义波动率
定义波动率参数的目的,是为了衡量资产价格在给定时期内上下波动的程度,为量化分析、投资决策、资产定价和风险管理提供科学依据。期权定价理论将股票价格抽象为随机变量,只能用刻画随机变量偏离均值离散程度的统计参数(标准差)来度量股票价格的波动程度,因而无法正确描述和度量股票价格的实际波动程度。
本文根据股票价格与时间之间「一一对应」的数量关系,将股票价格抽象为随机过程中的一条样本轨道,使用函数分析方法来度量股票价格的波动程度,同时还能正确度量风险和收益率的大小。
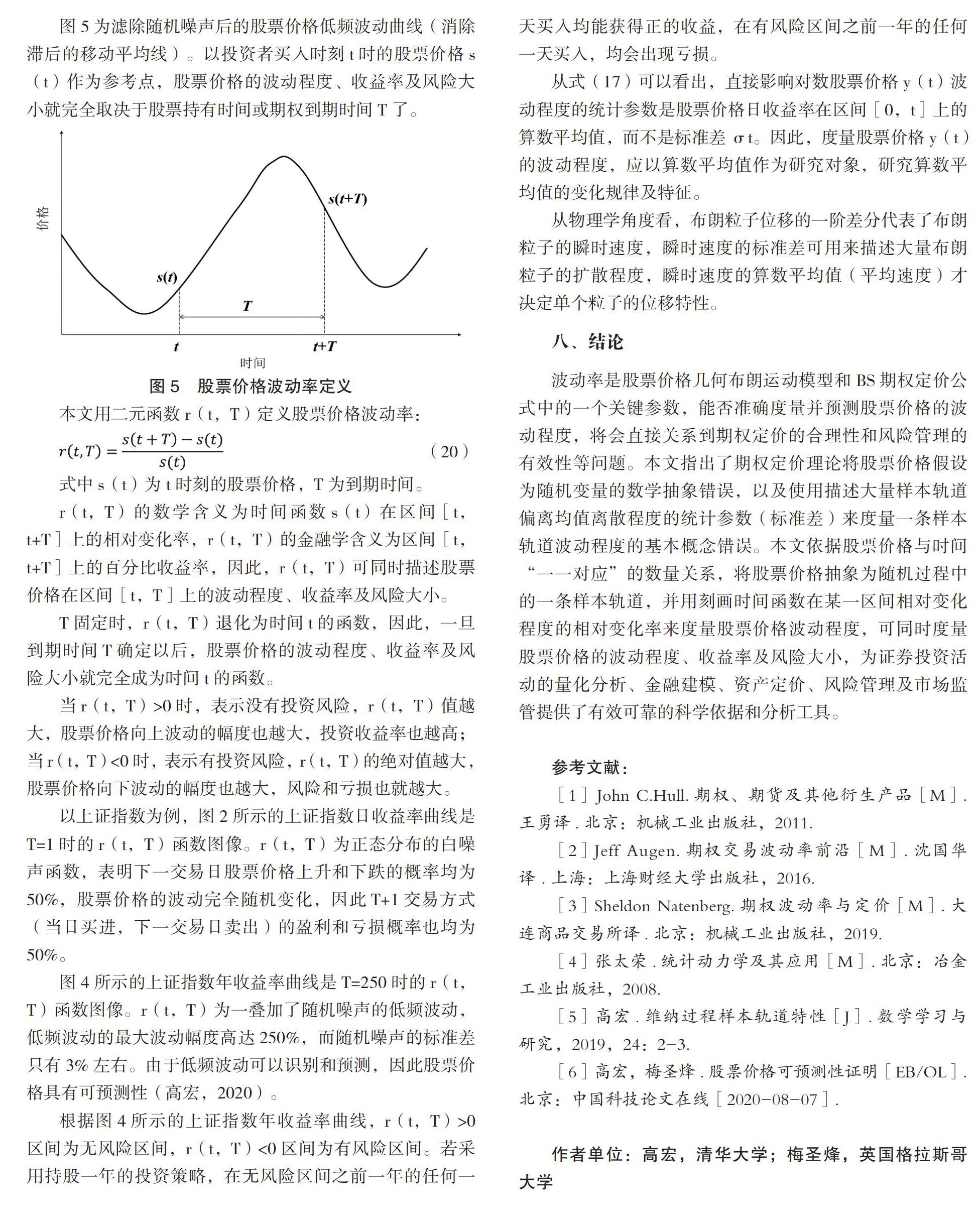
图 5 为滤除随机噪声后的股票价格低频波动曲线(消除滞后的移动平均线)。以投资者买入时刻 t 时的股票价格 s(t)作为参考点,股票价格的波动程度、收益率及风险大小就完全取决于股票持有时间或期权到期时间 T 了。
本文用二元函数 r(t,T)定义股票价格波动率:
(20)
式中 s(t)为 t 时刻的股票价格,T 为到期时间。
r(t,T)的数学含义为时间函数 s(t)在区间[t,t+T]上的相对变化率,r(t,T)的金融学含义为区间[t,t+T]上的百分比收益率,因此,r(t,T)可同时描述股票价格在区间[t,T]上的波动程度、收益率及风险大小。
T 固定时,r(t,T)退化为时间 t 的函数,因此,一旦到期时间 T 确定以后,股票价格的波动程度、收益率及风险大小就完全成为时间 t 的函数。
当 r(t,T)>0 时,表示没有投资风险,r(t,T)值越大,股票价格向上波动的幅度也越大,投资收益率也越高;当 r(t,T)<0 时,表示有投资风险,r(t,T)的绝对值越大,股票价格向下波动的幅度也越大,风险和亏损也就越大。
以上证指数为例,图 2 所示的上证指数日收益率曲线是 T=1 时的 r(t,T)函数图像。r(t,T)为正态分布的白噪声函数,表明下一交易日股票价格上升和下跌的概率均为 50%,股票价格的波动完全随机变化,因此 T+1 交易方式(当日买进,下一交易日卖出)的盈利和亏损概率也均为 50%。
图 4 所示的上证指数年收益率曲线是 T=250 时的 r(t,T)函数图像。r(t,T)为一叠加了随机噪声的低频波动,低频波动的最大波动幅度高达 250%,而随机噪声的标准差只有 3% 左右。由于低频波动可以识别和预测,因此股票价格具有可预测性(高宏,2020)。
根据图 4 所示的上证指数年收益率曲线,r(t,T)>0 区间为无风险区间,r(t,T)<0 区间为有风险区间。若采用持股一年的投资策略,在无风险区间之前一年的任何一天买入均能获得正的收益,在有风险区间之前一年的任何一天买入,均会出现亏损。
从式(17)可以看出,直接影响对数股票价格 y(t)波动程度的统计参数是股票价格日收益率在区间[0,t]上的算数平均值,而不是标准差 σt。因此,度量股票价格 y(t)的波动程度,应以算数平均值作为研究对象,研究算数平均值的变化规律及特征。
从物理学角度看,布朗粒子位移的一阶差分代表了布朗粒子的瞬时速度,瞬时速度的标准差可用来描述大量布朗粒子的扩散程度,瞬时速度的算数平均值(平均速度)才决定单个粒子的位移特性。
八、结论
波动率是股票价格几何布朗运动模型和 BS 期权定价公式中的一个关键参数,能否准确度量并预测股票价格的波动程度,将会直接关系到期权定价的合理性和风险管理的有效性等问题。本文指出了期权定价理论将股票价格假设为随机变量的数学抽象错误,以及使用描述大量样本轨道偏离均值离散程度的统计参数(标准差)来度量一条样本轨道波动程度的基本概念错误。本文依据股票价格与时间「一一对应」的数量关系,将股票价格抽象为随机过程中的一条样本轨道,并用刻画时间函数在某一区间相对变化程度的相对变化率来度量股票价格波动程度,可同时度量股票价格的波动程度、收益率及风险大小,为证券投资活动的量化分析、金融建模、资产定价、风险管理及市场监管提供了有效可靠的科学依据和分析工具。
参考文献:
[1]John C.Hull.期权、期货及其他衍生产品[M].王勇译.北京:机械工业出版社,2011.
[2]Jeff Augen.期权交易波动率前沿[M].沈国华译.上海:上海财经大学出版社,2016.
[3]Sheldon Natenberg.期权波动率与定价[M].大连商品交易所译.北京:机械工业出版社,2019.
[4]张太荣.统计动力学及其应用[M].北京:冶金工业出版社,2008.
[5]高宏.维纳过程样本轨道特性[J].数学学习与研究,2019,24:2-3.
[6]高宏,梅圣烽.股票价格可预测性证明[EB/OL].北京:中国科技论文在线[2020-08-07].
作者单位:高宏,清华大学;梅圣烽,英国格拉斯哥大学
作者 高宏 梅圣烽