沪深 300 股指期权推出对标的指数波动性的影响研究

摘要：2019 年 12 月 23 日，沪深 300 股指期权正式推出。基于沪深 300 指数五分钟高频交易数据，文章利用 ARMA-GARCH 模型实证检验了沪深 300 股指期权推出对标的指数波动性的影响。结果表明，沪深 300 股指期权正式推出后，标的指数波动率显着上升，表明期权的推出可能加剧标的指数的波动性。

关键词：股指期权 波动性 ARMA-GARCH 沪深 300

一、引言

2019 年 12 月 23 日，沪深 300ETF 期权和股指期权的上市仪式分别在沪深交易所和中金所举行。作为中国市场的首个指数期权，沪深 300 股指期权的上市完善了多层次市场体系，推动我国金融市场业务的发展以及金融产品的创新。

现有相关文献关于期权推出对标的市场波动性影响的研究并没有取得比较一致结论，沪深 300 指数相关期权的推出对指数波动性的影响仍有待进一步检验。一方面随着更多投资者和机构参与到沪深 300 的期权市场中，在看涨期权和看跌期权的作用下，沪深 300 期权的推出能够减少现货市场的波动性，推动我国资本市场稳定健康的发展。另一方面，沪深 300 期权的推出可能会使投资者和机构利用独特的做空机制进行投机，从而加大现货市场的波动性。对此，本文以沪深 300 指数为样本，研究沪深 300 股指期权的推出对标的指数波动性的影响。

二、文献回顾

国外衍生品起步较早、相关机制较为完善，国外学者对于该领域的研究也更为成熟。证券市场波动率的研究基本是基于 ARCH 族模型展开。Engle（1982）首先提出自回归条件异方差模型 ARCH 模型，Bollerslev（1986）则在 ARCH 模型上进行扩展，构建了自回归条件异方差模型 GARCH 模型。国外大量文献基于 ARCH 族模型的体系研究证券市场波动性。Nelson（1991）提出的 EGARCH 模型允许资产收益率对波动率有不对称的影响，放松了 GARCH 模型系数非负的限制。Zakoian（1994）则提出了 TGARCH 模型来刻画杠杆效应的波动率模型。

国内衍生品市场仍不完善，金融衍生产品品种也比较有限，国内学者早期基本都是对国外衍生品市场进行研究。例如，徐珊（2009）基于日经 225 指数期货推出的事件研究表明，股指期货的推出对现货市场的波动性没有明显的影响。王琦（2013）、郭海盼（2017）借助 GARCH 模型研究 KOSPI200 指数期权对标的指数波动性的影响，发现期权的上市会增大标的指数的波动性。在国内推出沪深 300 股指期货等金融衍生品后，不少学者开始研究国内的金融衍生品对标的价格波动的影响。刘瑾婧等（2011）、崔新亮（2012）、于帆（2013）等发现，沪深 300 股指期货的上市会加剧现货市场的波动性。徐金剑（2016）的研究表明，中证 500 股指期货加剧标的指数波动，而上证 50 股指期货则有助于减缓指数波动。

从现有研究来看，有关金融衍生品推出对标的价格波动影响的研究并没有得到比较一致的结论，而且目前也缺少关于我国沪深 300 指数相关期权推出对沪深 300 指数波动性影响的研究。因此，本文拟以沪深 300 指数相关期权上市作为事件，研究我国金融期权推出对标的波动性的影响，为我国进一步有序推出金融衍生品、维护金融市场稳定提供实证参考。

三、研究设计

（一）数据选取与变量说明

本文选取 2019 年 4 月 30 日至 2020 年 8 月 20 日的沪深 300 指数的 5 分钟高频数据作为研究样本，包含沪深 300 股指期权上市前后各 160 个交易日，共计 15，360 个 5 分钟级别数据。

金融市场中的波动性通常是指金融资产在一段时间内的变化，包括价格变化的频率、幅度以及价格变化的非趋势特征。在金融市场中，波动性与风险有着密切的联系。一些文献直接采用收益率的方差或标准差来衡量价格波动，但是这种传统的度量方法难以有效捕捉金融市场波动集聚等特征，也难以追踪市场波动的动态变化。本文拟采用 ARMA-GARCH 模型来沪深 300 股指期权推出对标的指数波动性的影响，即在 GARCH 模型的均值方程中使用 ARMA 过程，其方差方程则能有效地刻画沪深 300 指数的波动。

首先，计算沪深 300 指数 5 分钟收益率序列 Rt=ln（Pt）-ln（Pt-1），其中 Pt 为第 t 个 5 分钟沪深 300 指数收盘价。① 再次，利用如下 ARMA-GARCH 模型来刻画沪深 300 指数的波动：

（1）

其中，该模型的均值方程是一个 ARMA（m，n）过程，条件方差方程是一个 GARCH（p，q）过程。该模型方差方程对应的被解释变量（）较好地刻画了沪深 300 指数的波动。

（二）实证模型

为了检验沪深 300 指数的相关期权推出对标的指数波动的影响，我们拟以期权推出作为事件构建一个虚拟变量（Postt），期权推出之前 Postt=0，期权推出之后 Postt=1。进一步地，在模型（1）的方差方程中加入 Postt，并重新进行参数估计。即：

（2）

模型（2）中，Postt 的系数（λ）捕捉了沪深 300 指数相关期权的推出对沪深 300 指数波动性变化的影响。若 λ 显着小于 0 时，则意味着沪深 300 指数相关期权的推出有助于降低沪深 300 指数的波动性。相反，若 λ 显着大于 0，则说明期权的推出会加剧沪深 300 指数的波动性。

四、实证结果分析

（一）描述性统计

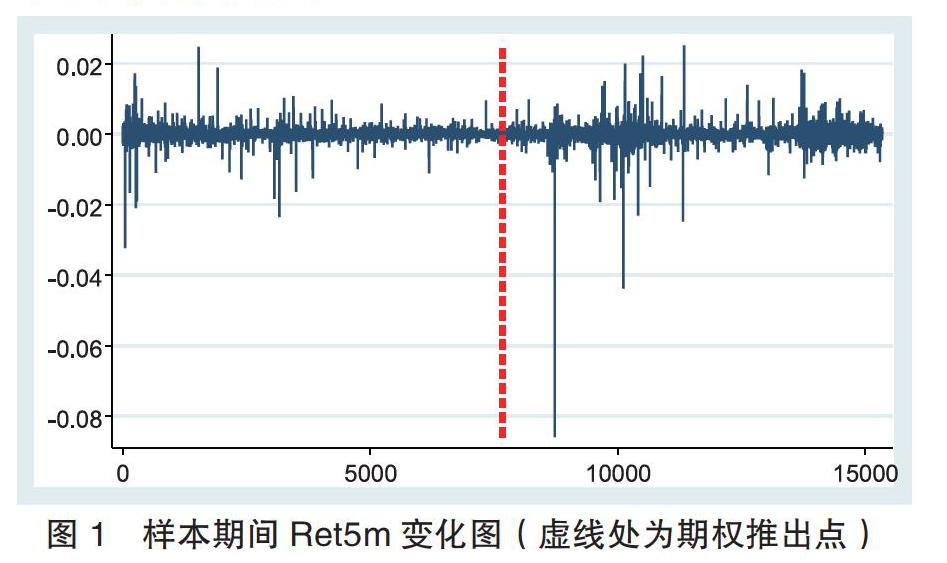
沪深 300 指数 5 分钟收益率序列（Rt）的峰度（358.29）远大于 3、偏度（-7.72）小于 0，说明该收益率序列呈现明显的左偏、尖峰分布，验证了股市收益率序列尖峰厚尾的特征。同时，Rt 的 J-B 检验值异常大，也意味着该收益率序列不服从正态分布。

从图 1 可以看出，收益率序列呈现明显的波动集聚的特点，不服从同方差假设。而且，从图中也可以看出，股指期权推出后，沪深 300 指数收益率序列的极端波动有所放大，很可能会加剧波动。

最后，为了防止出现伪回归，我们还对收益率序列进行 ADF 单位根检验。结果显示，收益率序列（Rt）的 ADF 值（-122.50）在 1% 的显着性水平下显着小于临界值，说明 Rt 是一个平稳的时间序列。

（二）回归结果

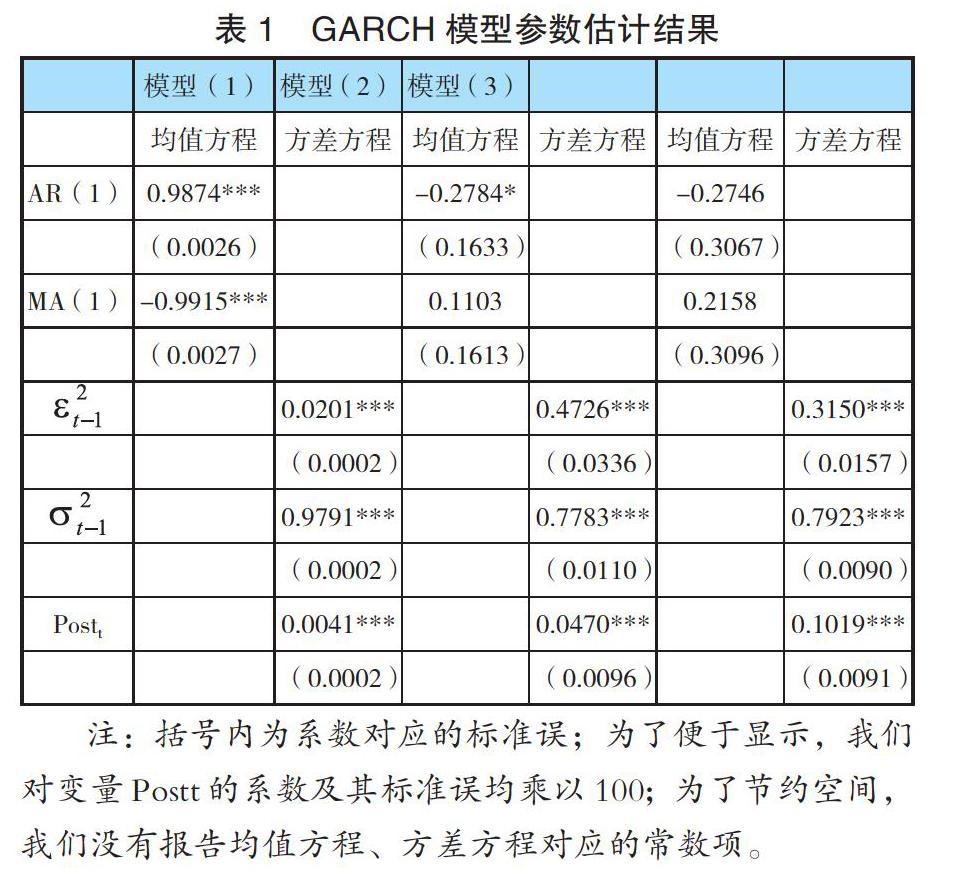
在利用 ARMA-GARCH 模型刻画沪深 300 指数波动率时，合理确定均值方程 ARMA 节数以及方差方程 ARCH 项、GARCH 项的阶数比较关键。利用 AIC、SC 准则，我们选择 ARMA（1，1）、GARCH（1，1）作为基准模型。在此基础上，我们在方差方程中加入代表期权推出的虚拟变量（Postt）并进行参数估计。表 1 的模型（1）报告了全样本回归的结果。从回归结果可以看出，Postt 的系数显着为正，意味着沪深 300 指数相关期权推出之后，标的指数（沪深 300 指数）的波动显着上升。表明沪深 300 指数期权的推出加剧了标的指数的波动。

为了检验结果的稳健性，我们还在进一步利用期权推出前后 1 个月、2 个月的 5 分钟数据进行参数估计。表 1 的模型（2）、模型（3）分别报告了利用前后 1 个月、2 个月数据的回归结果。从方差方程结果可以看出，模型（2）、模型（3）中 Postt 的回归系数均显着为正，这进一步证明了期权推出对标的指数波动性存在不利影响。进一步地，模型（1）中 Postt 的回归系数明显小于模型（2）、模型（3）中对应的回归系数，说明随着时间推移，期权推出对沪深 300 指数波动性的影响有所减弱。

五、结论与展望

基于沪深 300 指数 5 分钟高频数据，文本利用 ARMA-GARCH 模型实证检验了沪深 300 指数相关期权的推出对沪深 300 指数波动性的影响，并利用多个时间段来进行稳健性检验。实证结果表明，沪深 300 指数相关期权的推出显着加剧了沪深 300 指数的波动性。研究结果发现虚拟变量前的系数为正，沪深 300 股指期权的推出加大了沪深 300 指数的波动性。此外，多个时段的回归结果显示，沪深 300 指数相关期权推出对指数波动性的不利影响随时间推移有所减弱。

注释：

① 为了便于展示实证结果，我们对 Rt 做乘以 100 处理。

参考文献：

[1]Bollerslev T. Generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics，1986，31（3）：307-327.

[2]Engle R F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J]. Econometrica：Journal of the Econometric Society，1982：987-1007.

[3]Nelson D B. Conditional heteroskedasticity in asset returns：A new approach[J]. Econometrica：Journal of the Econometric Society，1991，59（2）：347-370.

[4]Zakoian J M. Threshold heteroskedastic models[J]. Journal of Economic Dynamics and control，1994，18（5）：931-955.

[5]崔新亮. 股指期货对股票指数波动性影响的实证研究[D]. 辽宁大学，2012.

[6]郭海盼. 韩国 KOSPI200 股指期权对标的指数波动性影响以及对我国的启示[D]. 北京外国语大学，2017.

[7]刘瑾婧，方兆本，李海涛. 中国股指期货的价格发现功能和波动外溢效应[J]. 中国科学技术大学学报，2011，41（9）：760-763.

[8]王琦. 股指期权对标的指数波动性影响研究[D]. 辽宁大学，2013.

[9]徐金剑. 股指期货对标的指数波动性影响分析——基于中证 500 股指期货[J]. 金融经济：下半月，2016 （5）：87-89.

[10]徐珊. 股指期货对股票价格指数波动性影响——对日经 225 指数的实证分析[J]. 中国证券期货，2009 （4X）：7-10.

[11]于帆. 我国沪深 300 股指期货对股票现货市场波动性影响研究[D]. 华中师范大学，2013.

[12]张孝岩，沈中华. 股指期货推出对中国股票市场波动性的影响研究——基于沪深 300 股指期货高频数据的实证分析[J]. 投资研究，2011，10：112-122.

基金项目：上海市「科技创新行动计划」软科学重点项目（项目编号：20692191700）。

作者单位：上海立信会计金融学院金融科技学

作者 黄嘉麒 吕大永