基于 GARCH 族模型的上证 50ETF 期权定价研究
 作者
作者


【摘要】考虑到金融资产日收益率分布普遍地存在显着的尖峰厚尾现象,且其波动率存在时变性特征,本文运用自回归条件异方差系列模型(GARCH 模型、TGARCH 模型和 EGARCH 模型)来建模上证 50ETF 收益的波动率,并应用于上证 50ETF 期权定价。数值结果表明:上证 50ETF 收益率波动存在明显的时变性特征;由 GARCH 族模型计算得到的期权价格,与真实价格之间不存在显着差异;此外,考虑了非对称性波动影响的 TGARCH 和 EGARCH 模型,要比 GARCH 模型能更好刻画现实市场波动率动态特性,从而取得了更高的期权定价准确度。
【关键词】GARCH 模型 TGARCH 模型 EGARCH 模型 期权定价 蒙特卡洛模拟
一、引言
金融衍生品挂牌交易,是基于通货膨胀、供需情况、汇率、利率及标的物价格未来走势的预期等信息基础上竞价成交的,因而交易价格的变化反映了市场的供需关系,是现货价格未来走势的重要信息来源,可为现货市场的成交价格提供重要的参考作用。此外,金融衍生工具不仅能够进行市场预期并发现价格,而且可以通过套期保值来降低价格风险。因此,自产生以来,金融衍生工具交易量呈逐年上升趋势,已经成为整个市场体系不可缺少的一个重要组成部分。经过多年的发展,我国的资本市场也不断地走向成熟,在经过长时间的筹备与模拟测试,我国首个期权合约品种「上证 50ETF 期权」终于应运而生,于 2015 年 2 月 9 日正式在上海证券交易所挂牌交易,个股期权等其他更多的交易品种也有望在年后推出,由此,2015 年也被称为是中国期权的元年。但是,由于我国期权市场刚刚成立,对于符合我国国情的金融衍生工具的定价研究仍较为缺乏。
国内外学术界对期权的定价理论研究有着很长的历史。1973 年由 Blake 和 Scholes 提出的传统的 B-S 模型是一个假设股票价格服从几何布朗运动,在无套利的分析框架下给出的期权定价公式[1]。Merton(1976)认为市场证券的价格分布往往并非是光滑移动的,而是呈现间断的「跳空」过程,提出了一种股票价格遵循跳跃过程的模型,在股票价格服从几何布朗运动之上加入了各种跳跃[2]。这两个模型中都包含了常数波动率假设,但是越来越多的实证研究结果表明,金融产品的收益率分布存在着显着的尖峰、厚尾和非对称等特征。同时,其波动率也并非常数,而具有时变性、波动聚集性。所以,放松波动率为常数的假设,研究波动率的动态变化特性,这对于提升期权定价的准确性具有重要意义。
针对这一内容,当前国内外很多学者都做出了不懈地努力,研究工作大体上可归为两大类:一是,为资产收益波动率构建适当的连续动态方程,如假设波动率为随机过程,Hull 和 White(1987)[3]、Scott(1987)[4]、Heston(1993)[5]等建立了随机波动率模型;Bates(1996)[6]和 Scott(1997)[7]建立了随机波动跳-扩散模型,该模型的优点是能较好刻画出隐含波动率的「微笑」与「偏斜」效应。然而,由于非交易的波动是不能任意用现存资产来复制,因此,波动率方程自身的模型误定风险(misspecificationerror)会使期权定价更加复杂化。尽管从数学角度可以通过一些不现实的假设来简化波动风险模型,但金融实践中要用此模型计算出期权定价,仍然需要使用复杂的数量方法。第二个分支是,利用时间序列方法来构建波动率的离散动力系统,如广义条件自回归(GARCH)系列模型{1}。GARCH 族模型在某种意义上可视为随机波动率模型的离散时间版本,其优点在于:能直接从股票的历史价格中得出收益波动率,而不必从同期其他期权推出内含波动率;此外,它具有一定的波动率预测功能。
自 GARCH 模型提出以后,人们自然联想到利用 GARCH 模型来定价期权。Duan(1995)通过局部风险中性定价关系(localrisk- neuralvaluationrelationship),建立了基于 GARCH 模型的离散时间序列的期权定价模型。Hardle 和 Hanfner(2000)在 Duan 的工作的基础上,应用 TGARCH 模型对德国市场期权进行定价,发现基于 TGARCH 模型的定价结果与 BS 模型和 GARCH 模型相比,更接近真实价格。Jong 和 Lehnert(2001)则认为 EGARCH 模型能较好地刻画不同期限的「波动率微笑」曲线,构建了一个估计指数期权局部波动率的 EGARCH 模型,并成功地解释和预测了实际的波动率[10]。王健,李超杰,何建敏(2006)建立了有交易成本的 GARCH 扩散期权定价模型[11]。LouisH.Ederington,WeiGuan(2007)对 GARCH 系列所有模型做了实证研究,发现 GARCH(1,1)和 TGARCH 模型在高波动的时间段内预测偏差特别大[12]。Christoffersen,Elkamhi,Feunou(2007)基于 Duan(1995)的 GARCH 模型,分析了条件非正态分布和条件正态分布下的定价差异,发现前者的定价效果要好于后者[13]。
然而,到目前为止,用 GARCH 族模型对上证 50ETF 期权进行定价研究的,并不多见,部分原因在于上证 50ETF 期权诞生时间非常短暂。因此,本文尝试在这方面做点工作,利用 GARCH 族模型对上证 50ETF 期权进行定价研究,试图通过比较三个模型的定价效果,探寻适用于我国现阶段 50ETF 期权市场的定价模型。
二、GARCH 族模型
(一)GARCH 模型
传统时间序列模型都假定波动率并不随时间变化的,但在现实市场中波动率具有时变性。Engle 提出的 ARCH 模型能够很好刻画波动率的这种时变特性。
对于某一时间序列 yt,其变化规律可由下述回归模型描述:
■ (1)
在 t 时刻可获得的信息集为 Ωt-1 的条件下,误差项 εt 遵循以 0 为期望、ht 为条件方差的正态分布,即 ■=0,■ 亦可写作 ■,其中 ■。
■ (2)
其中,■,且 ■,即条件方差具有 m 阶自回归形式,则称误差项 εt 服从 m 阶自回归条件异方差,记 ■ 过程。
上面定义的条件方差,可理解为在己知信息集为 Ωt-1(该信息集包括前期所有的误差项信息,如 ■ 的条件下,t 时刻干扰项 εt 的方差。对于由公式(2)表示的条件方差,表明前期的 m 阶误差项对本期误差项 εt 有着正向且持续的影响。通过该机制,当前期误差值较大时,本期误差值就较大;当前期误差值较小时,本期误差值就较小。由此较好的刻画了 ARCH 模型所描述的波动率集聚现象。当随机误差项具有异方差性,若用传统的最小二乘法估计就会产生偏差,若使用 ARCH 模型,则可提高预测精度,亦可知其准确性。当方差较大时,预测值的置信区间会较小,故具有较好的可靠性。
虽然 ARCH 模型较传统的时间序列模型有所改进,但是仍存在很多缺点,如在现实中应用 ARCH 模型,为了得到更好的拟合效果需要很大的阶数 m,这样不仅增大了计算量,还会带来诸如解释变量多重共线性等其他问题。为了修正 ARCH 模型的缺点,Bollerslev 在 1986 年对 ARCH 模型进行扩展,得到了 GARCH 模型:
■ (3)
由(3)式可看出,GARCH 模型与 ARCH 模型的不同之处在于:扰动项 εt 的条件方差不仅受到前期残差项平方(■)的影响外,还要受到条件方差滞后项(■)的影响。因此 GARCH 模型比 ARCH 模型更具有一般性。同时,ARCH 模型只是 GARCH(p,q)中 q=0 时的一个特例。GARCH 模型具有很强的概括能力,可以用低阶的 GARCH 模型来代表高阶的 ARCH 模型,从而使得模型的识别和估计都变得比较容易。
(二)EGARCH 模型
从式看,GARCH 模型确实在很大程度上解决了 ARCH 模型的一些缺陷,且具有较好的可操作性,但 GARCH 模型(3)依然存在一些缺陷而无法完全刻画金融时间序列波动率的特征,其中最重要的一个缺陷是:GARCH 模型没有反映「利空」消息和「利好」消息对股价产生非对称性冲击这个事实。为克服此缺陷,Nelson(1991)将市场信息的非对称影响效应融入到 GARCH 模型中,提出了指数 GARCH 模型,即 EGARCH 模型。
对于序列 ■,其中 ■,Vt 服从标准正态分布,即 Vt~N(0,1)。EGARCH(1,1)模型的条件方差方程可写成:
■ (4)
等式左边是条件方差的对数,这意味着杠杆影响是指数的,而不是二次的,所以条件方差的预测值一定是非负的。
非对称效应的存在能够通 ■ 过的假设得到检验。只要 ■,冲击的影响就存在着非对称性。
更高阶的 EGARCH(p,q)模型可表示为:
■ (5)
实际应用中,通常会对上述模型进行变换,由 ■,可得 ■,模型可变换为:
■ (6)
虽然式(6)和 Nelson 的模型(5)设定的不同,但是在对这两个模型进行估计而得到的结果中,系数 α 和 β 的估计量是相同的,不同的只是截距项 ω 的值,它将根据分布假设和阶数 p 的变化而变化,这并不影响分析的结果。同时 Nelson 假设 vt 的条件分布是服从广义误差分布(GED),而在实际应用中,可以允许其在正态分布、学生 t 分布和 GED 分布中进行选择。
(三)TGARCH 模型
与 EGARCH 模型目的相似,为刻画市场波动率的非对称效应,Zakoian(1994)提出了 TGARCH 模型,该模型中的条件方差方程被设定为:
■ (7)
其中 ■ 是一个虚拟变量,当 ■ 时,■;否则,■;只要 ■,就存在非对称效应。
在式(7)中,条件方差方程中的 ■ 项,称为非对称效应项,或 TGARCH 项。条件方差方程表明 ht 依赖于前期的残差平方 ■ 和条件方差 ■ 的大小。好消息(■>0)和坏消息(■<0)对条件方差产生不同的影响:好消息有一个 α 倍的冲击,即 ■>0 时,■=0,式(7)中的非对称项不存在;而坏消息则有一个 ■ 倍的冲击,这是因为,当 ■<0 时,■=1,此时非对称项出现。如果 γ>0,说明存在杠杆效应,利空消息对市场产生的冲击要比利好消息的程度大,即非对称效应的主要效果是使得波动加大;如果 γ<0,表明利好消息会带来更强的市场波动而利空消息会降低市场的波动,即非对称效应的作用是使得波动减小。
三、基于 GARCH 族模型的期权定价原理
下面主要以 Hardle 和 Hanfner(2000)构建的基于 TGARCH 模型的期权定价为例,阐述期权定价的基本原理。该文选择的风险溢价均值方程为:
■ (8)
式中,ω,α,β 是满足平稳条件的常数。λ 可以解释为每一风险的单位溢价。
模型(8)是在自然测度 P 下进行估计的。为得到风险中性测度 Q 下的鞅过程,Duan(1995)构造了一个新的误差项 ηt。ηt 加入了时变风险溢价,即 ■。在测度 Q 下,模型变为:
■ (9)
运用蒙特卡洛模拟的方法,模拟出基于 GARCH 模型(9)的风险资产价格时间序列。由于这是在风险中性概率的条件下进行模拟的,所以可以通过无风险利率对期末现金流进行贴现,这样就可以估算出期权的价值了。
值得一提的是,GARCH 模型的起始波动率 σ0 选择,对期权定价结果具有一定影响。本文采用现有文献普遍使用的稳态波动率,作为 GARCH 模型的起始波动率。由 GARCH 模型(9)知,稳态波动率 ■ 为 ■。
考虑到 GARCH 模型在我国证券市场的实证结果[14],证券收益均值方程一般写成
■
再应用 Duan(1995)方法,将上述方程转换为风险中性测度 Q 下标的资产价格方程,即
■ (10)
其中 νt 为标准正态分布随机变量。
最后,通过迭代就能得到期权到期日 T 时刻的价格 PT。从而,由蒙特卡洛模拟方法得到的期权价格可表达为:
■ (11)
其中 M 为独立仿真的资产价格路径数。
基于 EGARCH 和 TGARCH 模型的期权定价方法与上面基本类似,仅波动率的计算方法有所不同。在此不再赘述。
四、数值实验
(一)数据选取
关于基础标的资产,本文选用 2005 年 2 月 23 日-2015 年 4 月 7 日上证 50ETF 每日收盘价(共计 2459 个数据)作为原始数据,并基于此构建 GARCH 族模型。考虑到在此期间内上证 50ETF 的分红派息等会导致权益变化,进而导致价格的非交易性变动,因此本文选取复权后的收盘价作为本文的数据源。
由于上证 50ETF 期权在我国是新鲜事物,可用的历史数据并不长。为避免「新鲜事物效应」对期权价格的影响,本文刻意选取该期权已稳定运行一段时间后的市场数据:选取距离到期日 2015 年 4 月 22 日还有 10 个交易日{2}(即采样 2015 年 4 月 8 日)的 4 月份看涨期权的收盘价数据。选择超短到期的期权数据,原因在于:第一,距离到期日时间越短,期权价格对波动率的敏感程度越强;第二,国际市场上超短到期的期权交易活跃,应用也很广。因此,分析这样的期权价格将更加具有现实意义。
此外,考虑到流动性与期权价格的关系,本文只选取成交量大于等于 1000 份的期权价格数据,原因是交投活跃的期权交易可能驱使出较为合理的成交价格。
由于看跌期权可以通过期权的平价定理与看涨期权进行相互的转化,所以本文不选取看跌期权数据。
关于无风险利率的选取,本文选择一年定期银行存款利率作为无风险利率,根据中国银行最新公布的一年定期银行存款利率,本文取 r=2.75%。当然,也可选取其他利率,如 Shibor,作为无风险利率。但这并不对本文最后结论构成任何实质性影响。
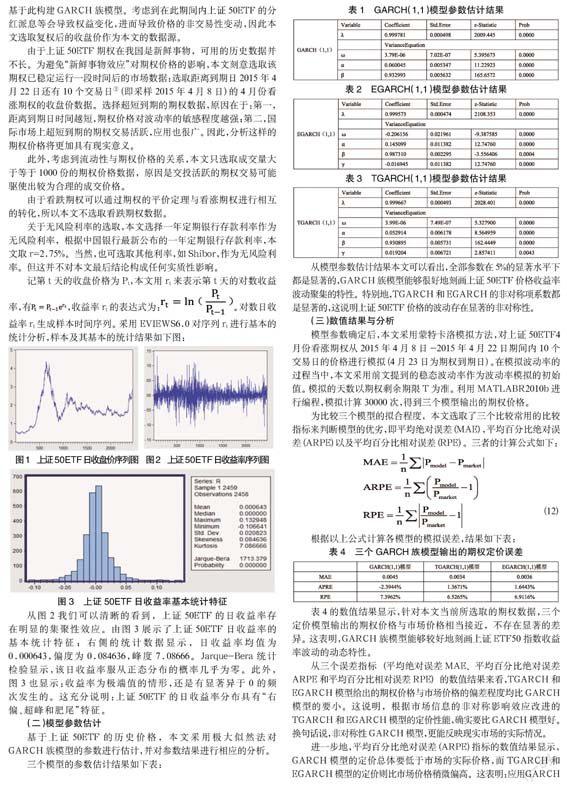
记第 t 天的收盘价格为 Pt,本文用 rt 来表示第 t 天的对数收益率,有 ■,收益率 rt 的表达式为:■。对数日收益率 rt 生成样本时间序列。采用 EVIEWS6.0 对序列 rt 进行基本的统计分析,样本及其基本的统计结果如下图:
从图 2 我们可以清晰的看到,上证 50ETF 的日收益率存在明显的集聚性效应。由图 3 展示了上证 50ETF 日收益率的基本统计特征;右侧的统计数据显示,日收益率均值为 0.000643,偏度为 0.084636,峰度 7.08666。Jarque-Bera 统计检验显示,该日收益率服从正态分布的概率几乎为零。此外,图 3 也显示:收益率为极端值的情形,还是有显着异于 0 的频次发生的。这充分说明:上证 50ETF 的日收益率分布具有「右偏、超峰和肥尾」特征。
(二)模型参数估计
基于上证 50ETF 的历史价格,本文采用极大似然法对 GARCH 族模型的参数进行估计,并对参数结果进行相应的分析。
三个模型的参数估计结果如下表:
从模型参数估计结果本文可以看出,全部参数在 5% 的显着水平下都是显着的,GARCH 族模型能够很好地刻画上证 50ETF 价格收益率波动聚集的特性。特别地,TGARCH 和 EGARCH 的非对称项系数都是显着的,这说明上证 50ETF 价格的波动存在显着的非对称性。
(三)数值结果与分析
模型参数确定后,本文采用蒙特卡洛模拟方法,对上证 50ETF4 月份看涨期权从 2015 年 4 月 8 日-2015 年 4 月 22 日期间内 10 个交易日的价格进行模拟(4 月 23 日为期权到期日)。在模拟波动率的过程当中,本文采用前文提到的稳态波动率作为波动率模拟的初始值。模拟的天数以期权剩余期限 T 为准。利用 MATLABR2010b 进行编程,模拟计算 30000 次,得到三个模型输出的期权价格。
为比较三个模型的拟合程度,本文选取了三个比较常用的比较指标来判断模型的优劣,即平均绝对误差(MAE),平均百分比绝对误差(ARPE)以及平均百分比相对误差(RPE)。三者的计算公式如下:
■ (12)
根据以上公式计算各模型的模拟误差,结果如下表:
表 4 的数值结果显示,针对本文当前所选取的期权数据,三个定价模型输出的期权价格与市场价格相当接近,不存在显着的差异。这表明,GARCH 族模型能够较好地刻画上证 ETF50 指数收益率波动的动态特性。
从三个误差指标(平均绝对误差 MAE、平均百分比绝对误差 ARPE 和平均百分比相对误差 RPE)的数值结果来看,TGARCH 和 EGARCH 模型给出的期权价格与市场价格的偏差程度均比 GARCH 模型的要小。这说明,根据市场信息的非对称影响效应改进的 TGARCH 和 EGARCH 模型的定价性能,确实要比 GARCH 模型好。换句话说,非对称性 GARCH 模型,更能反映现实市场的实际情况。
进一步地,平均百分比绝对误差(ARPE)指标的数值结果显示,GARCH 模型的定价总体要低于市场的实际价格,而 TGARCH 和 EGARCH 模型的定价则比市场价格稍微偏高。这表明:应用 GARCH 模型对上证 ETF50 指数收益的波动特性建模,将可能会产生「波动率泄漏」问题,从而低估期权价格;而 TGARCH 和 EGARCH 模型则总体上高估波动率。有趣的是,本研究可能揭示出一种可能的针对上证 ETF50 期权的校准方法:即结合 GARCH 模型和 TGARCH(或 EGARCH)模型二者的定价结果。
最后,考察 GARCH 族模型在实值期权(ITM,inthemoney)定价和虚值期权(OTM,outofthemeney)定价性能上的差异,以进一步评判基于 GARCH 族模型的期权定价适用宽度。表 5 给出了基于 GARCH、TGARCH 和 EGARCH 模型的 ITM 和 OTM 看涨期权的定价误差。
表 5 中的结果清晰地反映出,三个 GARCH 族模型对实值期权的定价效果均表现出色,平均百分比相对误差(RPE)都在 3% 左右。然而,对于虚值期权的定价效果,在完全相同参数设置下,三个模型的定价性能表现,均相应地比对实值期权进行定价的效果要差。原因其实也一目了然地反映在表 5 中:对于参数确定的 GARCH 族模型,其输出的实值期权和虚值期权的绝对定价误差,在数量上无显着差别;但由于虚值期权在数值上本身就非常小,往往较接近于 0,因此,相对误差就显得额外大。要提高 GARCH 族模型在虚值期权上定价精度,一种简便有效的方法是:提高模型的阶数。注意到:表 4 和表 5 中的 GARCH 族模型,p=q=1。表 6 给出了当 p=2,q=1 时,三个 GARCH 族模型对虚值期权的定价效果。
表 6 中结果显示,提升阶数后的三个 GARCH 族模型对虚值期权的定价效果都一定程度的改善,具体体现为三个误差指标都降低,如平均百分比相对误差(RPE)比低阶模型给出的结果降低了 2%~3%,这说明提高模型的阶数确实能够提升三个 GARCH 族模型对虚值期权的定价效果。
五、结论
本文基于 GARCH 族模型对上证 50ETF 期权进行数值定价,得到以下结论:
一是总体来说,GARCH 模型、TGARCH 模型以及 EGARCH 模型给出的期权数值价格与实际价格,均不存在显着的差异。这表明:GARCH 族模型能较好地刻画上证 50ETF 指数收益率的波动特性。
二是考虑了市场信息非对称冲击效应的 GARCH 改进模型,如 TGARCH 和 EGARCH 模型,其定价性能明显优于不作改进的 GARCH 模型。这本质上表明,「利空」消息和「利好」消息确实对上证 50ETF 指数波动产生非对称性的冲击效应。
三是在完全相同参数设置下,GARCH 族模型在实值期权上的定价性能,要略优于在虚值期权上的定价表现。要提高 GARCH 族模型在虚值期权上定价精度,一种简便有效的方法是:提高模型的阶数。
注释
{1}Engle(1982)提出了自回归条件异方差(ARCH)模型,其假定收益率残差服从条件正态分布,条件期望为零,条件方差为以前若干期收益率误差平方的函数[8]。但该模型存在拟合时阶数过大等问题。于是 Bollerslev(1986)在 ARCH 型中引入无穷期误差项,得到广义自回归条件异方差(GARCH)模型。Duan(1995)发表了 GARCH 期权定价模型,以 GARCH(Generalized Autoregressive Conditional Heteroscedasticity)模型描述资产收益轨迹,反映了标的资产条件波动性的改变[9]。在此基础上,考虑到风险溢价随时间变化而变化的因素,Engle,Lilien&Robbins;(1987)提出了 ARCH-M 模型。尽管如此,仍然无法解决利空消息和利好消息对股价产生不同冲击的问题,考虑到波动率的非对称性,Nelson(1991),Zakoian(1994)分别给出了 EGARCH 和 TGARCH 模型。
{2}这里特地关注「交易日」,而不是自然日,是因为用 GARCH 模型做时间序列仿真,仿真时长对应的是「总的交易日」,而非自然日。
参考文献
[1]Black,Scholes.Thepricing of options and corporate liabilities[J].Journal of political economy,1973,3(81):637-659.
[2]Merton.Option pricing when underlying stock returns are discontinuous[J].Journal of Financial Economics,1976,3(2):125-144.
[3]Hull,White.Thepricing of options on assets with stochastic volatilities[J].The Journal of Finance,1987,2(42):281-299.
[4]Scott LO.Option pricing when the variance changes randomly:theory estimation and an application[J]. Journal of Financial and Quantitative Analysis,1987,22(1):419-438.
[5]Heston SL.A Closed Solution For Options With Stochastic Volatility,With Application to Bond and Currency Options[J].Review of Financial Studies,1993,6(2):327-343.
[6]DBates.Jump and Stochastic Volatility:Exchange Rate Processes Implict in Deutche Markin Options[J]. Review of Financial Studies,1996,9(1):69-107.
[7]LScott.ricing Stock Optionsina Jump-Diffusion Model with Stochastic Volatility and Interest Rates:Applications of Fourier Inversion Methods[J].Mathematical Finance,1997,7(4):413-424.
[8]Engle.Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation [J].Econometrica,1982,50(4):987-1008.
[9]Duan,Jin-Chuan.The Garch option pricing model[J].Mathematical Finance,1995,5(31):13-32.
[10]Jong,Lehnert.Implied GARCH Volatility Forecasting[EB/OL].http://papers.ssrn.com,2001.
[11]王健,李超杰,何建敏.有交易成本的 GARCH-扩散期权定价模型[J].东南大学学报:自然科学版,2006,36(1): 174-178.
[12]Louis,Wei Guan.Time Series Volatility Forecasts for Option Valuation and Risk Management[R].AFA 2008 New Orleans Meetings Paper,2008.
[13]Christoffersen,Elkamhi,Feunou.JACOBS Option Valuation with Conditional Heteroskedasticity and Non-Normality [EB/OL].http://papers.ssrn.com/sol3,2007.
[14]何红霞,胡日东.中国股市价格的波动性研究——基于沪深 300 指数的 GARCH 族模型[J].和田师范大学学报,2010,29(3): 10-12.
[15]刘旭彬.GARCH 模型的蒙特卡罗模拟方法及应用[J].统计与决策,2010,2010(23):163-165.
[16]郑振龙,黄薏舟.波动率预测:GARCH 模型与隐含波动率[J].数量经济技术经济研究,2010,2010(1):140-150.
[17]李云红,魏宇.我国钢材期货市场波动率的 GARCH 族模型研究[J].数理统计与管理,2013,32(1):191-201.
[18]吴鑫育,周海林,汪寿阳,马超群.基于 GARCH 扩散模型的权证定价[J].系统工程理论与实践,2012,32(3):449-457.
作者简介:张浩林(1992-),男,广东佛山人,硕士研究生,研究方向:计算金融、量化投资。
作者 张浩林