基于 GARCH—VaR 模型对我国股票市场的风险度量研究

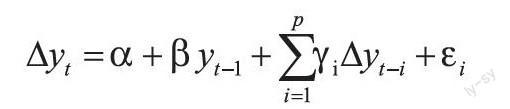
一、前言

自 20 世纪 70 年代以来，金融市场的波动日益加剧；80 年代以后，国际资本流动加剧，世界性金融风险和金融危机变得更加突出。90 年代，随着国际金融市场的日趋规范、壮大，各金融机构之间的竞争也发生了根本性变化。1988 年《巴塞尔协议》的诞生，该协议通过对不同类型资产规定不同权数来量化风险，是对银行风险比较笼统的一种分析方法。因此引发了各银行对风险管理的研究。

但是，这些传统方法很难准确定义和度量金融机构存在的金融风险。以往的风险衡量技术都只能适用于特定的金融工具或在特定的范围内使用，这些方法都难以综合反映风险承担的情况。风险监管者越来越需要一种既便于掌握和理解，又能全面反映金融机构所承担的市场风险的技术方法。VaR（Value-at-Risk，风险价值）方法正是在此背景下应运而生。

本文将选用 GARCH-VaR 方法对金融市场所面临的金融市场风险进行刻画，对沪深 300 最近两年的日收盘价进行考察，从实证的角度分析金融机构在金融市场上所暴露的风险。

二、模型介绍

（一）VaR 模型的介绍

1.VaR 的定义及数学表达。VaR（Value at Risk）的含义是「处在风险中的价值」，即在险价值，指的是资产价值中暴露于风险的部分。用数学公式可表示为：

其中：α 为给定的置信度，ΔVΔt 为投资组合在持有期 Δt 内的损失：VaR 为置信水平下处于风险中的价值。

2.VaR 的计算。

（1）方差-协方差方法。

假定持有期内资产价值的变化与其风险因素报酬成线性关系，风险因素报酬均服从正态分布。即：

其中：Pt-1 表示前一期的资产实际价值，Zα 表示置信水平为 α 下的资产收益率分布的分位数，ht 为资产收益率的条件方差，反映了资产收益波动率，t 为持有天数。

因而，计算 VaR 的关键在于计算出第 t 期资产回报率的方差。目前，主要有两种方法估计方差：简单移动平均法（SMA）、指数加权移动平均法（EWMA）

SMA 的数学表达式：；或者

在简答移动平均法中赋予了相等的权重；假设信息的权重随着时间成指数衰减，即赋予近期的数据较高的权重，赋予远期数据较低的权重，就得到了 EWMA 方法：

EWMA 的数学表达式：

（2）分析法（GARCH 族模型）。

分析法利用 GARCH 族模型来刻画资产收益率系列的条件异方差效应、非对称现象以及杠杆效益，选择不同的分布函数刻画资产收益率序列的尖峰厚尾特征，使其具有比较好的拟合效果。同时参数假设资产收益率服从某一特定的分布，极大程度的简化了 VaR 的计算，也越来越被大多数人所接受，成为计算 VaR 值得主流计算方法。具体的 GARCH 模型将在下面进行详细介绍。

（二）GARCH 类模型的简介

1.ARCH 模型。为克服了传统模型线性处理数据的缺陷，解决金融时间序列残差的异方差问题。经济学家 Engle 在 1982 年提出了自回归条件异方差 ARCH 模型（autoregressive conditional heteroscedasticity），大量的实践证明，ARCH 模型是较好地刻画金融资产收益数据的分布波动特性。

ARCH（p）模型的一般形式为：

2.GARCH 模型。为克服 ARCH 模型中的上述缺点，计量经济学家 Bollerslev 在 1986 年提出了着名的 GARCH 类模型。该模型的一般形式为 GARCH（p，q）：

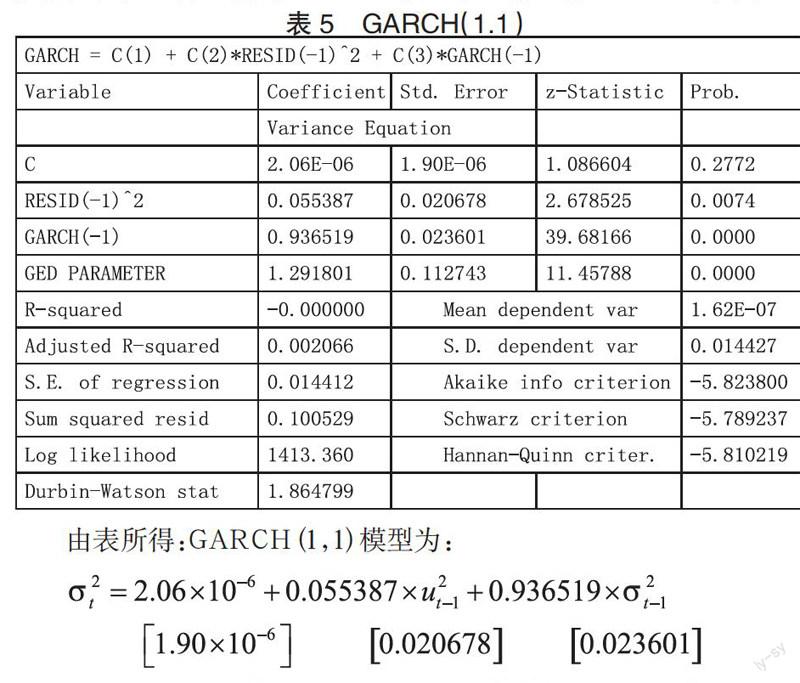
为了分析 GARCH 模型额特点，方便起见，取其中最为简单的 GARCH（1，1）模型为代表来分析模型，GARCH（1，1）模型的条件方差等式为：

三、实证研究

（一）数据选取与数据说明

本文选取了从 2013 年 6 月 1 日至 2015 年 5 月 31 日共 2 年的沪深 300 指数收盘价的数据，剔除没有交易的交易日后，沪深 300 指数收盘价的数据个数共为 485 个。

在金融研究中，人们普遍关注的是价格的变动而引起的收益率的变动而并非是价格本身，因此，本文将沪深 300 的收盘价转化为收益率序列来度量资产的在险价值。

对日收益率取自然对数可适当降低其异方差性，可以使得时间序列更易平稳，有利于建模因此，基于以上原因，本文采用几何收益率 Ri=lnPt-lnPt-1。

（二）基本数据的统计检验

1.正态检验。如果假定该收益率是服从正态分布则可以先找到在给定置信水平下的一个分位点，求出相对应的收益率，所以我们将对收益率进行正态检验，看是否服从正态分布。

（1）Jarque-Bera 检验。

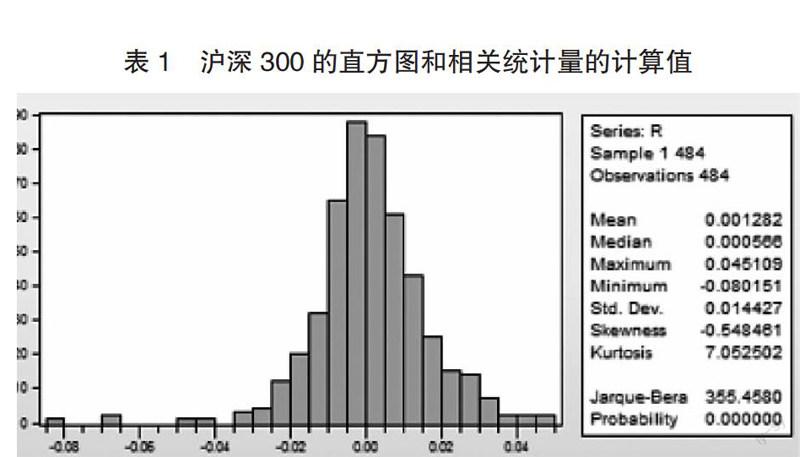
用 eviews 得到的描述性统计量如下图

由图可知：沪深 300 的 S 为-0548461，不为 0，则说明该分布有着较长的左拖尾，K 为 7.052502 大于 3，说明该分布的凸起程度（峰度）大于正态分布，Jarque-Bera 统计量为 355.4580，P 值为 0，拒绝原假设，即沪深 300 的分布不符合正态分布。

2.平稳性检验（单位根检验）。ADF：考虑序列 y 存在 P 阶序列相关，通过添项和减项的方法，将因变量的滞后项加入方程中：

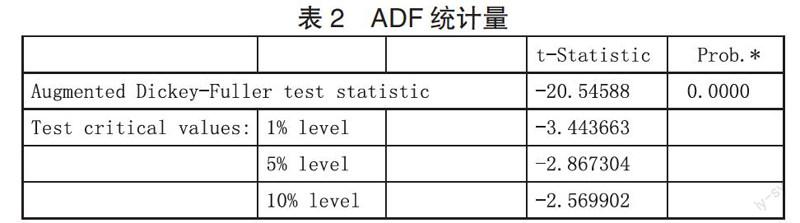
判断：若 ADF 值大于临界值，则接受原假设，意味着该时间序列存在单位根，必须对其进行差分处理，否则时间序列不平稳。如果 ADF 值小于临界值，则拒绝原假设，认为该事件序列是平稳的。

由上表的计算可知，ADF 统计量的值均小于显着性水平在 1%、5%、10% 下的临界值，所以拒绝原假设，认为该时间序列不存在单位根，即该时间序列是平稳的。

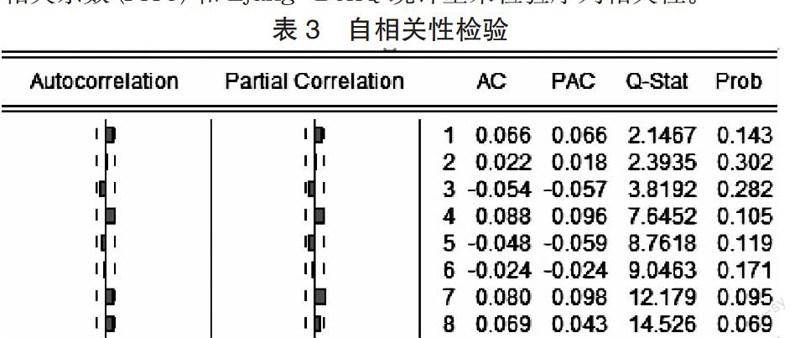
3.自相关性检验。自相关性检验主要为了检验在序列的临近数据之间存在多大程度的相关性，即收益率序列各期数据之间是否存在相关性。本文通过收益率序列滞后各期的自相关系数（AC）、偏自相关系数（PAC）和 Ljung-BoxQ 统计量来检验序列相关性。

由表可知，在 5% 的置信度下，相关系数都不显着等于 0，序列{R1}不具有自相关性，因此将其 GARCH 模型的均值方程均设定成白噪声。

4.异方差性。根据前文的收益率序列的时序图可以看出，收益率序列的波动具有明显的时变性，即某一特征的值会成群出现，扰动项的条件方差依赖于其前一期的大小，其随机扰动项在较大幅度波动后伴随着较大幅度的波动，较小幅度的波动后紧接着小幅度的波动。因此需要对收益率序列进行异方差的检验，即 ARCH 检验。

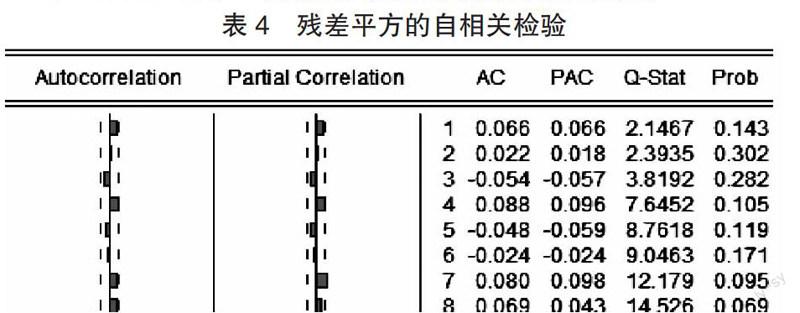
检验 ARCH 的方法有两种：一是 LM（拉格朗日乘数检验法）和对残差的方法相关图检验，由于本文中并没有对 ARMA 建模，在 EVIEWS 中没有直接的 LM 法，所以采用第二种，因此构建序列 w=（r-0.001282）。二是得到残差平方项的自相关检验。

由表可得，残差平方项的滞后一阶不具有自相关性之外，二阶以后均具有自相关性，因此可以认定，收益率序列具有异方差性。

5.GARCH 模型的建立。在建立 GARCH 族模型时，首先要对 GARCH 族模型中的残差分布进行假设，GARCH 族模型中的残差分布通常有正态分布、t 分布和广义误差分（GED）这三种假设，然后根据检验值选择适合的 GARCH 模型。一般选择 GARCH（1，1）

6.ARCH-LM 检验。下面，对回归结果进行滞后一阶的 ARCH-LM 检验，即 ARCH 检验：

由表可知，0.1597>0.05 的显着性水平，因此沪深 300 对数收益率序列不再具有 ARCH 效应，即 GARCH（1，1）模型可以消除上证综指对数收益率残差序列的条件异方差。

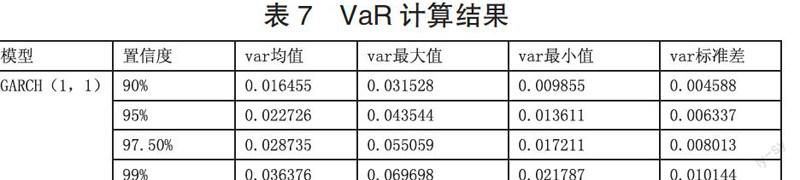
7.VaR 的计算。根据 VaR 的计算公式：

其中：置信度为 90% 的 GED 分布的分位数为 1.19251192258，置信度为 95% 的 GED 分布的分位数为 1.6469834324，置信度为 97.5% 的 GED 分布的分位数为 2.08250840205，置信度为 99% 的 GED 分布的分位数位 2.63623604358。

四、结论

本文以沪深 300 指数为例，来探讨如何将 VaR 方法引入我国金融机构的股市风险的度量中。经过对沪深 300 指数的对数收益率序列的检验中发现，该序列存在异方差效应不服从正态分布。因此本文建立了 GARCH 模型来更好的描述该序列的波动性，并且通过计算 VaR 来达到度量股市风险的效果。

近年来，随着我国金融市场的不断完善以及金融的快速发展，金融的监管水平以及风险管理水平也得到了很大的提升。当然，我国市场风险管理制度和方法上还存在着很多缺陷和不足，如市场风险管理的方法和技术比较落后，市场风险信息披露制度不健全，我国风险管理体系不够完善等等。利率市场化的逐步推进与股份制改革以及一系列的金融衍生工具的推出都使得我国金融市场的波动性增强，需要更精确的风险管理工具。

参考文献

[1]JP Morgan.Riskmetrics-Technical document[M].3th Edition，Morgan Guaranty Trust Company Global Research，1994.

[2]Jean-Philippe Bouch，Marc Potters.Worse fluctuation method for Fust Value-at-risk Estimates[J].The American Economic Review， 1997.

[3]Dowd，Kewin.Beyond Value-at-risk：The New Science of Risk Management[M].New York：Jogn Wiley and Sons，1998.

[4]Mike K.P.So， Philip L.H.Yu. Empirical analysis of GARCH models in value at risk estimate[J]， Journal of International Financial Markets，Institutions and Money，2008.

[5]Tardivo G.，Value at Risk：The New Benchmark for Managing Market Risk[J].Journal of Financial Management and Analysis，2002.

[6]李丽.基于 VaR 的我国商业银行利率风险度量研究[D].上海师范大学，2011.

[7]徐彬.VaR 模型在我国商业银行利率风险管理中的应用研究[D].南京工业大学，2008.

[8]史天雄.VaR 方法及其在中国股票市场的风险度量研究[J].中国地质大学学报，2010.

[9]黄伟男.GARCH-VAR 在银行外汇管理中的应用[J].金融视线，2013.

作者 沈一凡